



Minima/ maxima (statement questions) - Geometry questions
Minima/ maxima (statement questions) - Geometry questions
Last updated at Dec. 16, 2024 by Teachoo





Transcript
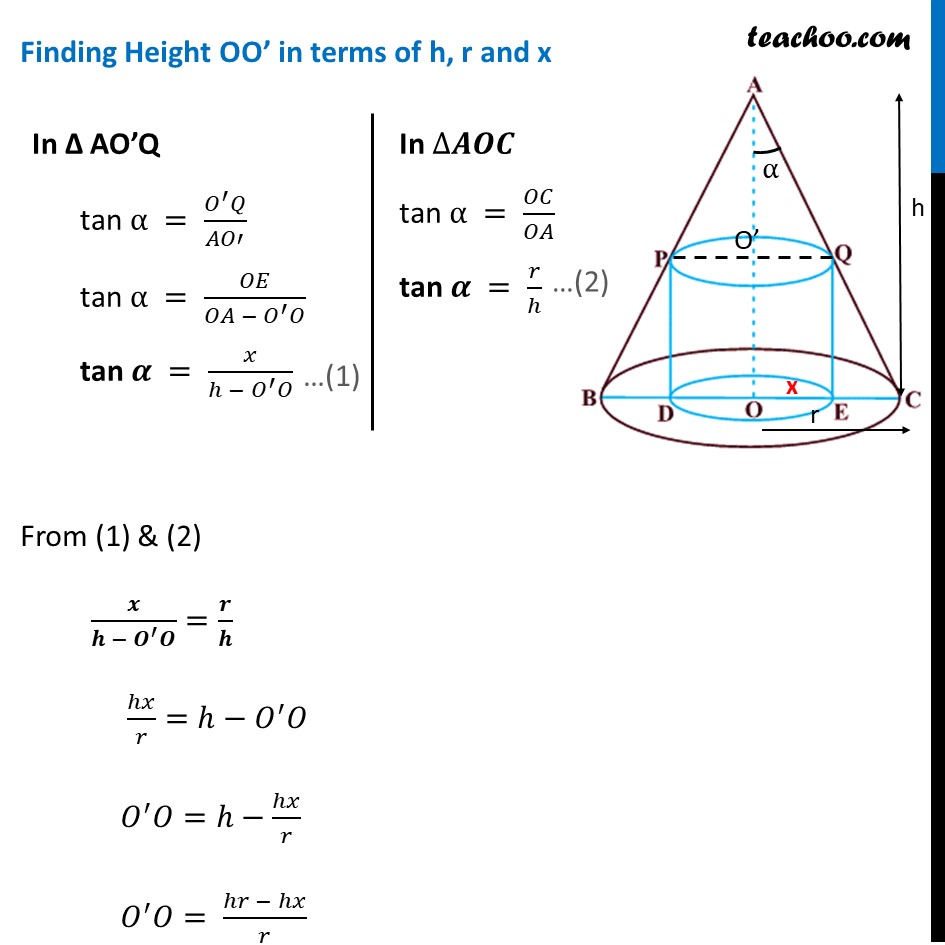
Example 26 Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that cone. Let OC = r be the radius of cone & OA = h be height of cone & ∠ OAQ = α be the semi-vertical angle of cone And, Let OE = x be the radius of cylinder Height of cylinder = OO’ Since cone is given, radius (r) and height (h) of cone are constant And, radius (x) and height (OO’) of cylinder is variable In Δ AO’Q tan α = (𝑂^′ 𝑄)/𝐴𝑂′ tan α = 𝑂𝐸/(𝑂𝐴 − 𝑂^′ 𝑂) tan 𝜶 = 𝑥/(ℎ − 𝑂^′ 𝑂) In ∆𝑨𝑶𝑪 tan α = 𝑂𝐶/𝑂𝐴 tan 𝜶 = 𝑟/ℎ Finding Height OO’ in terms of h, r and x From (1) & (2) 𝒙/(𝒉 − 𝑶^′ 𝑶)=𝒓/𝒉 ℎ𝑥/𝑟=ℎ−𝑂^′ 𝑂 𝑂^′ 𝑂=ℎ−ℎ𝑥/𝑟 𝑂^′ 𝑂= (ℎ𝑟 − ℎ𝑥)/𝑟 𝑶^′ 𝑶= 𝒉(𝒓 − 𝒙)/𝒓 Now, Curved Surface Area of Cylinder = 2𝜋 × Radius × Height S = 2𝜋" × " 𝑥" × " 𝑂^′ 𝑂 S = 2𝜋𝑥 ℎ(𝑟 − 𝑥)/𝑟 S = 2𝜋ℎ/𝑟 (𝑟𝑥−𝑥^2 ) S = 𝒌(𝒓𝒙−𝒙^𝟐 ) We need to minimize S Finding S’(x) S’ (x) = 𝑑(𝑘(𝑟𝑥 − 𝑥^2 ))/𝑑𝑥 S’ (x) = 𝑘 𝑑(𝑟𝑥 − 𝑥^2 )/𝑑𝑥 S’ (x) = 𝑘(𝑟−2𝑥) Putting S’ = 0 0 = 𝑘(𝑟−2𝑥) 𝑟−2𝑥 = 0 𝒙 = 𝒓/𝟐 Finding S’’(x) at x = 𝒓/𝟐 S’’ (x) = 𝑑(𝑘(𝑟 − 2𝑥))/𝑑𝑥 S’’ (x) = 𝑘 𝑑(𝑟 − 2𝑥)/𝑑𝑥 S’’ = 𝑘 (0−2) S’’ = −2𝑘 Therefore, S’’ (x) < 0 for 𝑥=𝑟/2 Thus, 𝒙=𝒓/𝟐 is maxima of S. Hence, radius of cylinder with greatest curved surface area which can be inscribed in a given cone is half of that cone