Example 25 - Chapter 6 Class 12 Application of Derivatives (Important Question)

Transcript

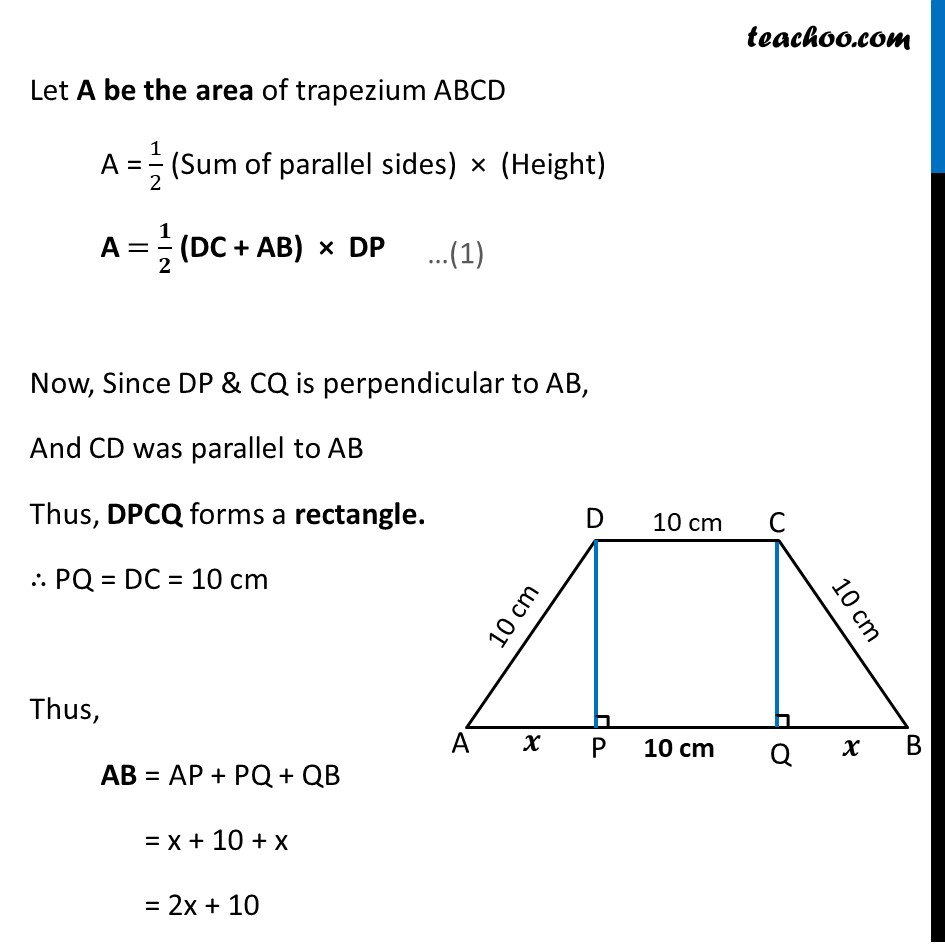
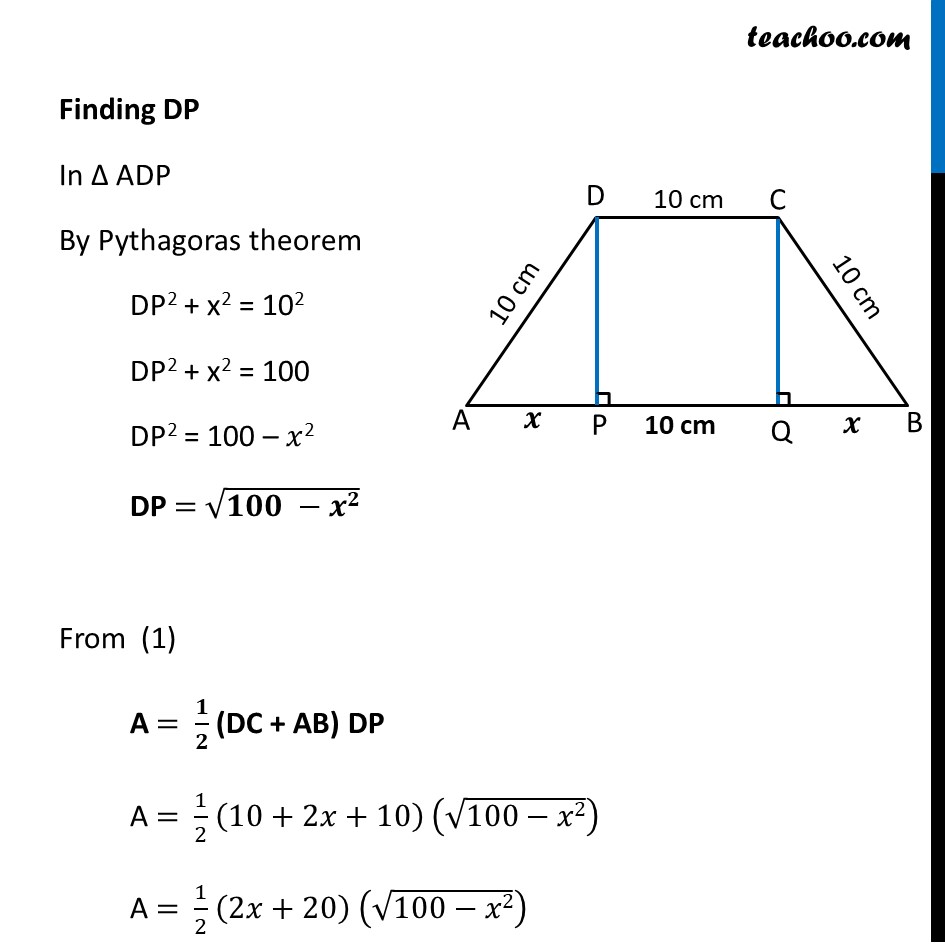
Example 25 If length of three sides of a trapezium other than base are equal to 10 cm, then find the area of the trapezium when it is maximum.Let ABCD be given trapezium Given length of sides other than base is 10 ∴ AD = DC = CB = 10cm. Draw a perpendicular DP & CQ on AB. Let AP = 𝒙 cm By symmetry QB = 𝒙 cm Let A be the area of trapezium ABCD A = 1/2 (Sum of parallel sides) × (Height) A = 𝟏/𝟐 (DC + AB) × DP Now, Since DP & CQ is perpendicular to AB, And CD was parallel to AB Thus, DPCQ forms a rectangle. ∴ PQ = DC = 10 cm Thus, AB = AP + PQ + QB = x + 10 + x = 2x + 10 Finding DP In Δ ADP By Pythagoras theorem DP2 + x2 = 102 DP2 + x2 = 100 DP2 = 100 – 𝑥2 DP = √(𝟏𝟎𝟎 −𝒙𝟐) From (1) A = 𝟏/𝟐 (DC + AB) DP A = 1/2 (10+2𝑥+10) (√(100−𝑥2)) A = 1/2 (2𝑥+20) (√(100−𝑥2)) A = (2(𝑥 +10) (√(100 − 𝑥2)))/2 A = (𝒙+𝟏𝟎) √(𝟏𝟎𝟎−𝒙𝟐) We need to find area of trapezium when it is maximum i.e. We need to Maximize Area A = (𝑥+10) (√(100−𝑥2)) Since A has a square root It will be difficult to differentiate Let Z = A2 = (𝑥+10)^2 (100−𝑥2) Since A is positive, A is maximum if A2 is maximum So, we maximize Z = A2 Differentiating Z Z =(𝑥+10)^2 " " (100−𝑥2) Differentiating w.r.t. x Z’ = 𝑑((𝑥 + 10)^2 " " (100 − 𝑥2))/𝑑𝑘 Z’ = [(𝑥 + 10)^2 ]^′ (100 − 𝑥^2 )+(𝑥 + 10)^2 " " (100 − 𝑥^2 )^′ Z’ = 2(𝑥 + 10)(100 − 𝑥^2 )−2𝑥(𝑥 + 10)^2 Z’ = 2(𝑥 + 10)[100 − 𝑥^2−𝑥(𝑥+10)] Z’ = 2(𝑥 + 10)[100 − 𝑥^2−𝑥^2−10𝑥] Z’ = 2(𝑥 + 10)[−2𝑥^2−10𝑥+100] Z’ = −4(𝑥 + 10)[𝑥^2+5𝑥+50] Putting 𝑑𝑍/𝑑𝑥=0 −4(𝑥 + 10)[𝑥^2+5𝑥+50] =0 (𝑥 + 10)[𝑥^2+5𝑥+50] =0 (𝑥 + 10) [𝑥2+10𝑥−5𝑥−50]=0 (𝑥 + 10) [𝑥(𝑥+10)−5(𝑥+10)]=0 (𝑥 + 10)(𝑥−5)(𝑥+10)=0 (𝑥 + 10)(𝑥−5)(𝑥+10)=0 So, 𝑥=5 & 𝑥=−10 Since 𝑥 represents distance & distance cannot be negative So, 𝒙 = 5 only By First Derivative Test Hence, 𝑥 = 5 is point of Maxima ∴ Z is Maximum at 𝑥 = 5 That means, Area A is maximum when x = 5 Finding maximum area of trapezium A = (𝑥+10) √(100−𝑥2) = (5+10) √(100−(5)2) = (15) √(100−25) = 15 √75 = 75√3 Hence, maximum area is 75√𝟑 cm2