Example 36 - Chapter 6 Class 12 Application of Derivatives

Transcript

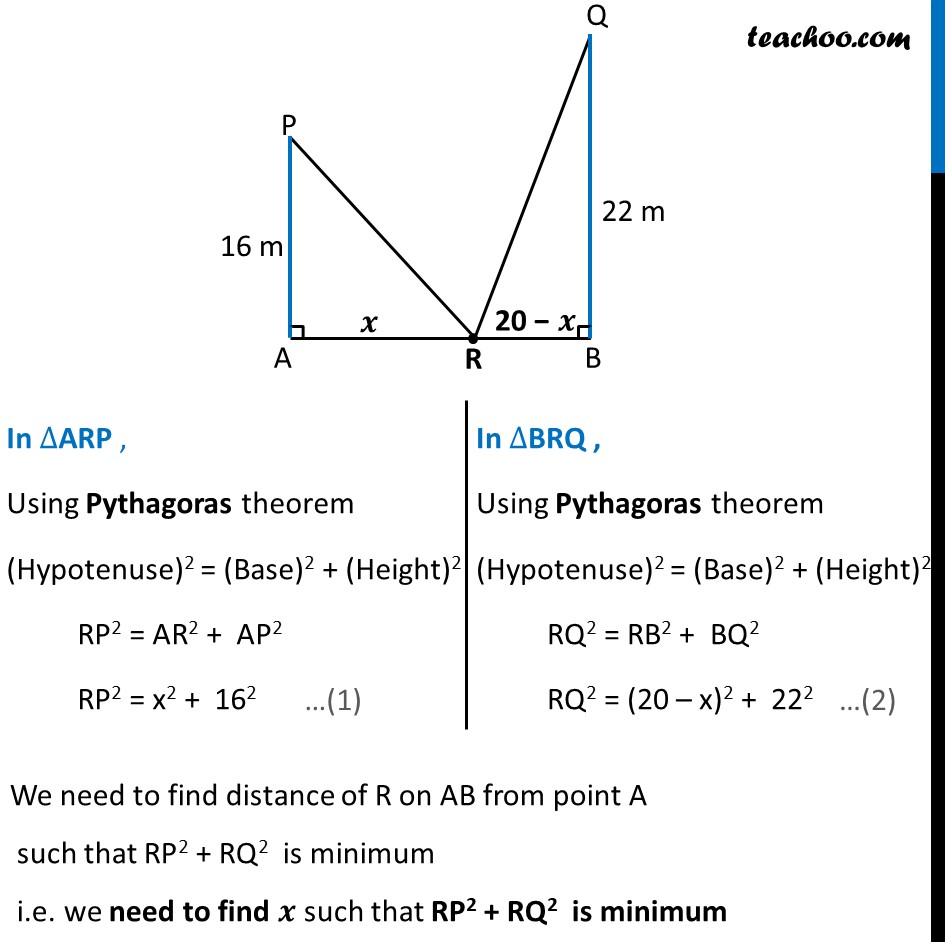
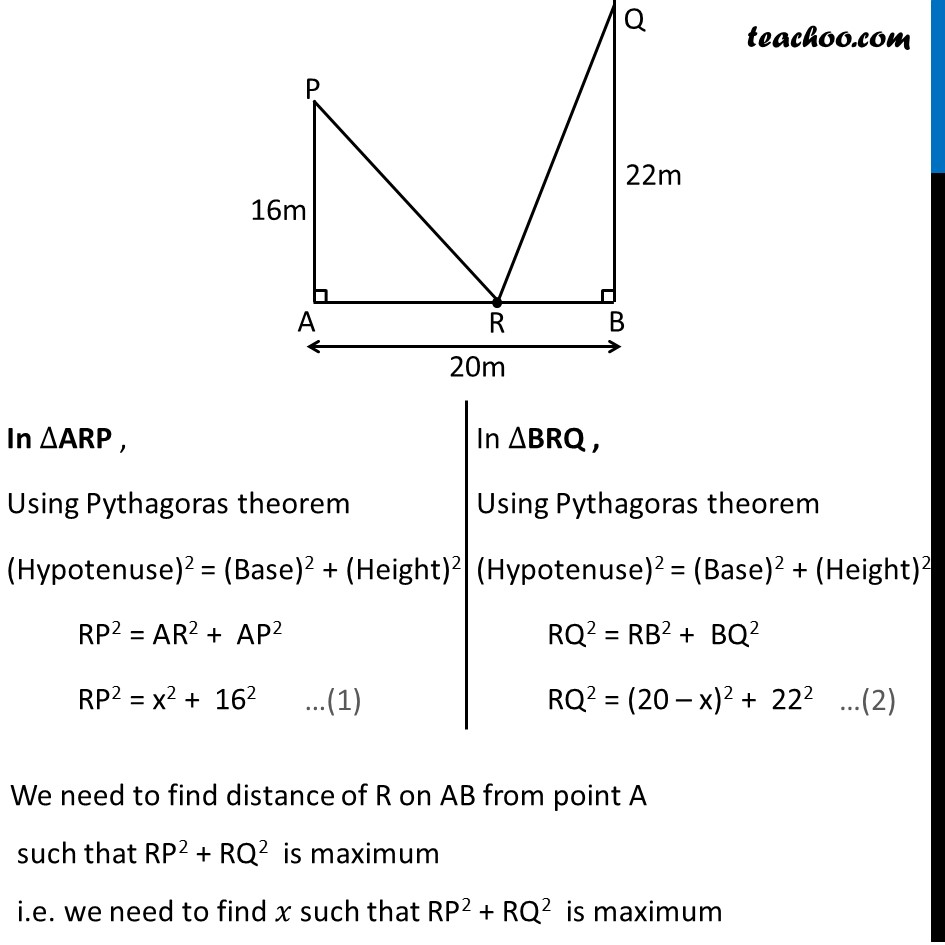
Example 36 Let AP and BQ be two vertical poles at points A and B, respectively. If AP = 16 m, BQ = 22 m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP2 + RQ2 is minimumGiven AP & BQ be two poles where AP = 16m, BQ = 22m & AB = 20m Let R be a point on AB Let AR = 𝒙 m. RB = AB – AR RB = 20 – 𝒙 Here, ∠ A = 90° & ∠ B = 90° as they are vertical poles In ∆ARP , Using Pythagoras theorem (Hypotenuse)2 = (Base)2 + (Height)2 RP2 = AR2 + AP2 RP2 = x2 + 162 In ∆BRQ , Using Pythagoras theorem (Hypotenuse)2 = (Base)2 + (Height)2 RQ2 = RB2 + BQ2 RQ2 = (20 – x)2 + 222 We need to find distance of R on AB from point A such that RP2 + RQ2 is minimum i.e. we need to find 𝒙 such that RP2 + RQ2 is minimum In ∆ARP , Using Pythagoras theorem (Hypotenuse)2 = (Base)2 + (Height)2 RP2 = AR2 + AP2 RP2 = x2 + 162 In ∆BRQ , Using Pythagoras theorem (Hypotenuse)2 = (Base)2 + (Height)2 RQ2 = RB2 + BQ2 RQ2 = (20 – x)2 + 222 We need to find distance of R on AB from point A such that RP2 + RQ2 is maximum i.e. we need to find 𝑥 such that RP2 + RQ2 is maximum Let S(x) = RP2 + RQ2 From (1) & (2) S(x) = 𝑥^2+(16)^2+(20−𝑥)^2+(22)^2 = 𝑥^2+(16)^2+(20−𝑥)^2+(22)^2 = 𝑥^2+256+((20)^2+(𝑥)^2−2(20)(𝑥))+484 = 𝑥^2+256+(400+𝑥^2−40𝑥 )+484 = 〖𝟐𝒙〗^𝟐−𝟒𝟎𝒙+𝟏𝟏𝟒𝟎 Finding S’(𝒙) S’(𝑥)=𝑑(2𝑥^2 − 40𝑥 + 1140)/𝑑𝑥 S’(𝑥)=4𝑥−40+0 S’(𝑥)=4(𝑥−10) Putting S’(𝒙)=𝟎 4(𝑥−10)=0 𝑥−10=0 𝒙=𝟏𝟎 Finding S’’(𝑥) S’’(𝑥)=4 𝑑(𝑥 − 10)/𝑑𝑥 S’’(𝑥)=4(1−0) S’’(𝑥)=4 Since S’’(𝑥)>0 at 𝑥=10 ∴ 𝒙=𝟏𝟎 is point of minima Hence, S(𝑥) is minimum when 𝑥=10 Thus, the distance of R from A on AB is AR = x = 10 𝒎