Ex 6.2,19 (MCQ) - Chapter 6 Class 12 Application of Derivatives

Transcript

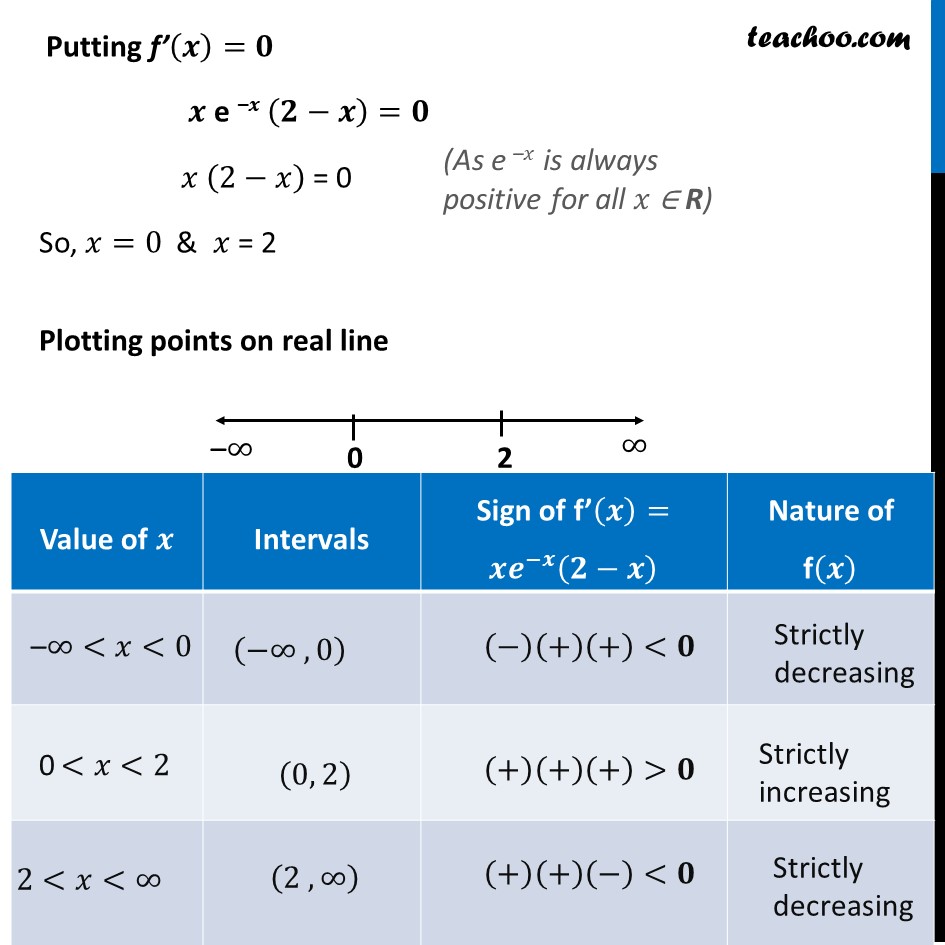
Ex 6.2, 19 The interval in which 𝑦 = 𝑥2 𝑒^(–𝑥) is increasing is (A) (– ∞, ∞) (B) (– 2, 0) (C) (2, ∞) (D) (0, 2)Let f(𝑥) = 𝑥^2 𝑒^(−𝑥) Finding f’(𝒙) f’(𝑥) = (𝑥^2 𝑒^(−𝑥) )′ Using product rule f’(𝑥) = (𝑥2)′ 𝑒^(−𝑥) + (𝑒^(−𝑥) )’ (𝑥2) f’(𝑥) = (2𝑥) 𝑒^(−𝑥) + (〖−𝑒〗^(−𝑥) ) (𝑥2) f’(𝑥) = 2𝑥 𝑒^(−𝑥)−𝑒^(−𝑥) 𝑥2 f’(𝒙) = 𝒙 e –𝒙 (𝟐−𝒙) Putting f’(𝒙)=𝟎 𝒙 e –𝒙 (𝟐−𝒙)=𝟎 𝑥 (2−𝑥) = 0 So, 𝑥=0 & 𝑥 = 2 Plotting points on real line (As e –𝑥 is always positive for all 𝑥 ∈ R) Hence, f(𝑥) is strictly increasing on (0 , 2) Therefore, correct answer is (𝐃)