Ex 6.2,15 - Chapter 6 Class 12 Application of Derivatives

Transcript

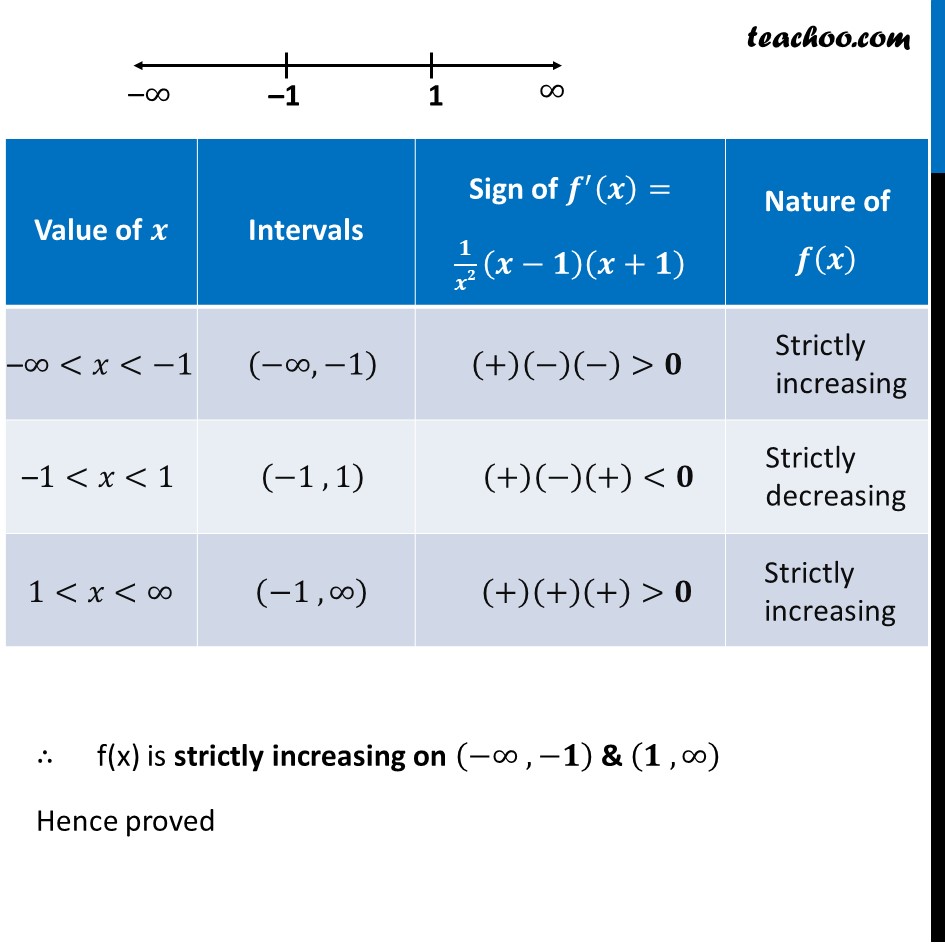
Ex 6.2, 15 Let I be any interval disjoint from [–1, 1]. Prove that the function f given by 𝑓(𝑥) = 𝑥 + 1/𝑥 is strictly increasing on I.I is any interval disjoint from [–1, 1] Let I = (−∞, −𝟏)∪(𝟏, ∞) Given f(𝑥) = 𝑥 + 1/𝑥 We need to show f(𝑥) is strictly increasing on I i.e. we need to show f’(𝒙) > 0 for 𝑥 ∈ (−∞, −𝟏)∪(𝟏, ∞) Finding f’(𝒙) f(𝑥) = 𝑥 + 1/𝑥 f’(𝑥) = 1 – 1/𝑥2 f’(𝑥) = (𝑥2 − 1)/𝑥2 Putting f’(𝒙) = 0 (𝑥2 − 1)/𝑥2 = 0 𝑥2−1 = 0 (𝑥−1)(𝑥+1)=0 So, 𝒙=𝟏 & 𝒙=−𝟏 Plotting points on number line The point 𝑥 = –1 , 1 into three disjoint intervals ∴ f(x) is strictly increasing on (−∞ , −𝟏) & (𝟏 , ∞) Hence proved