
Last updated at December 16, 2024 by Teachoo



Transcript
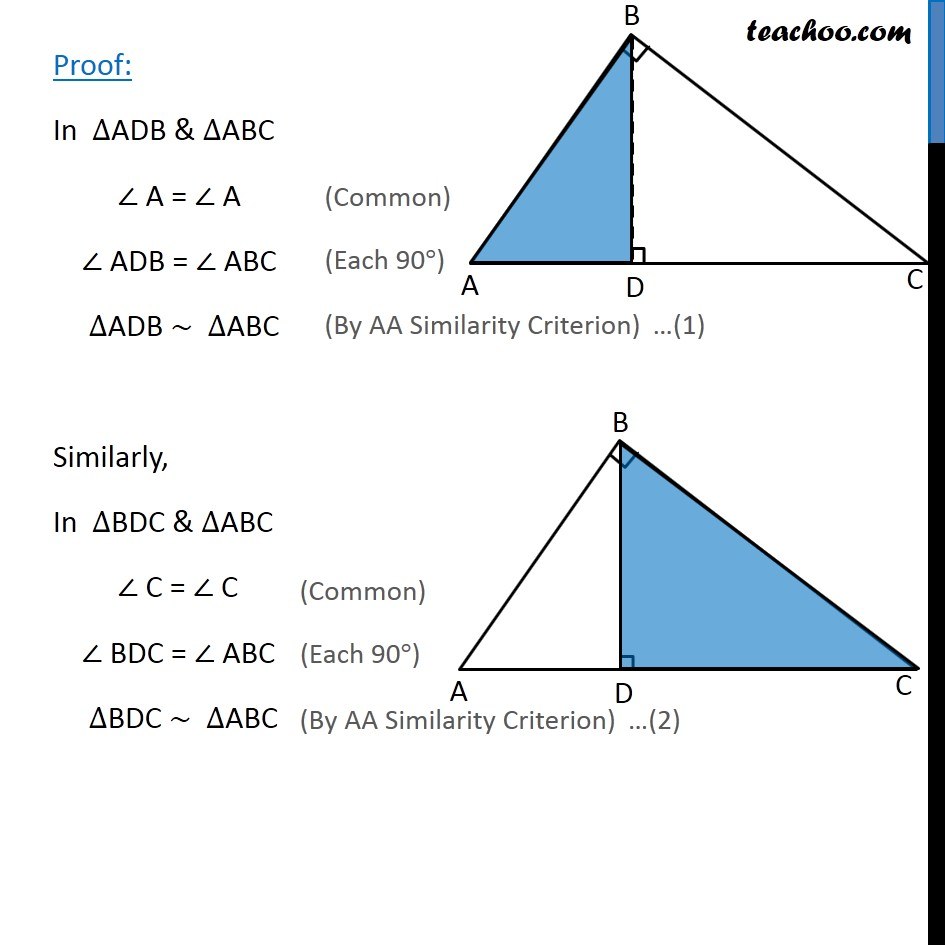
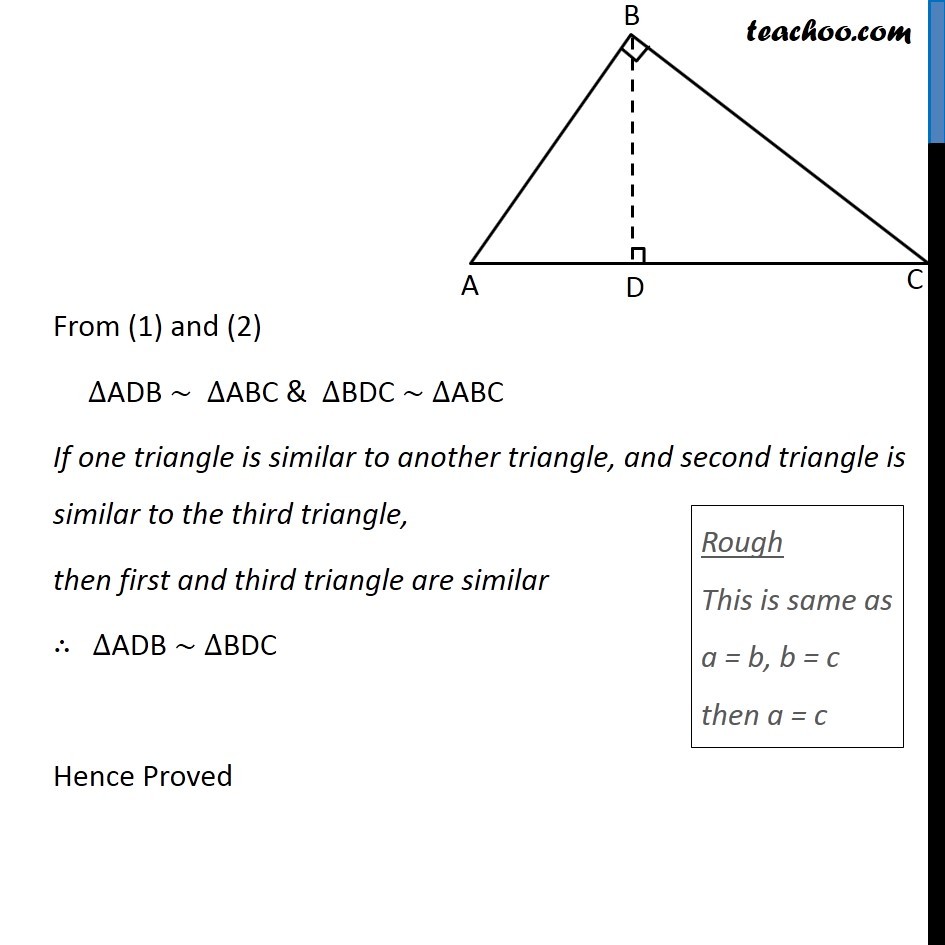
Theorem 6.7: If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then right triangle on both sides of the perpendicular are similar to the whole triangle and to each other Given: ∆ABC right angled at B & perpendicular from B intersecting AC at D. (i.e. BD ⊥ AC) To Prove: ∆ADB ~ ∆ABC ∆BDC ~ ∆ABC & ∆ADB ~ ∆BDC Theorem 6.7: If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then right triangle on both sides of the perpendicular are similar to the whole triangle and to each other Given: ∆ABC right angled at B & perpendicular from B intersecting AC at D. (i.e. BD ⊥ AC) To Prove: ∆ADB ~ ∆ABC ∆BDC ~ ∆ABC & ∆ADB ~ ∆BDC Proof: In ∆ADB & ∆ABC ∠ A = ∠ A ∠ ADB = ∠ ABC ∆ADB ~ ∆ABC Similarly, In ∆BDC & ∆ABC ∠ C = ∠ C ∠ BDC = ∠ ABC ∆BDC ~ ∆ABC From (1) and (2) ∆ADB ~ ∆ABC & ∆BDC ~ ∆ABC If one triangle is similar to another triangle, and second triangle is similar to the third triangle, then first and third triangle are similar ∴ ∆ADB ~ ∆BDC Hence Proved Rough This is same as a = b, b = c then a = c