Theorem 6.6 - Chapter 6 Class 10 Triangles

Transcript

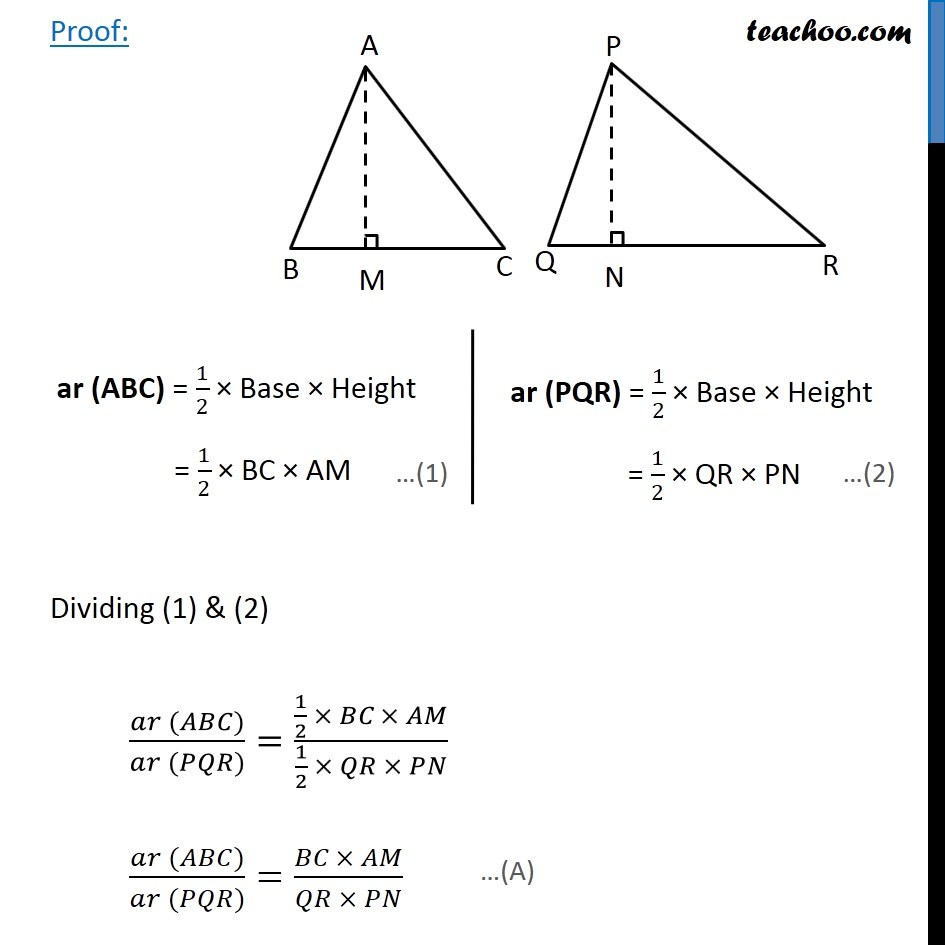
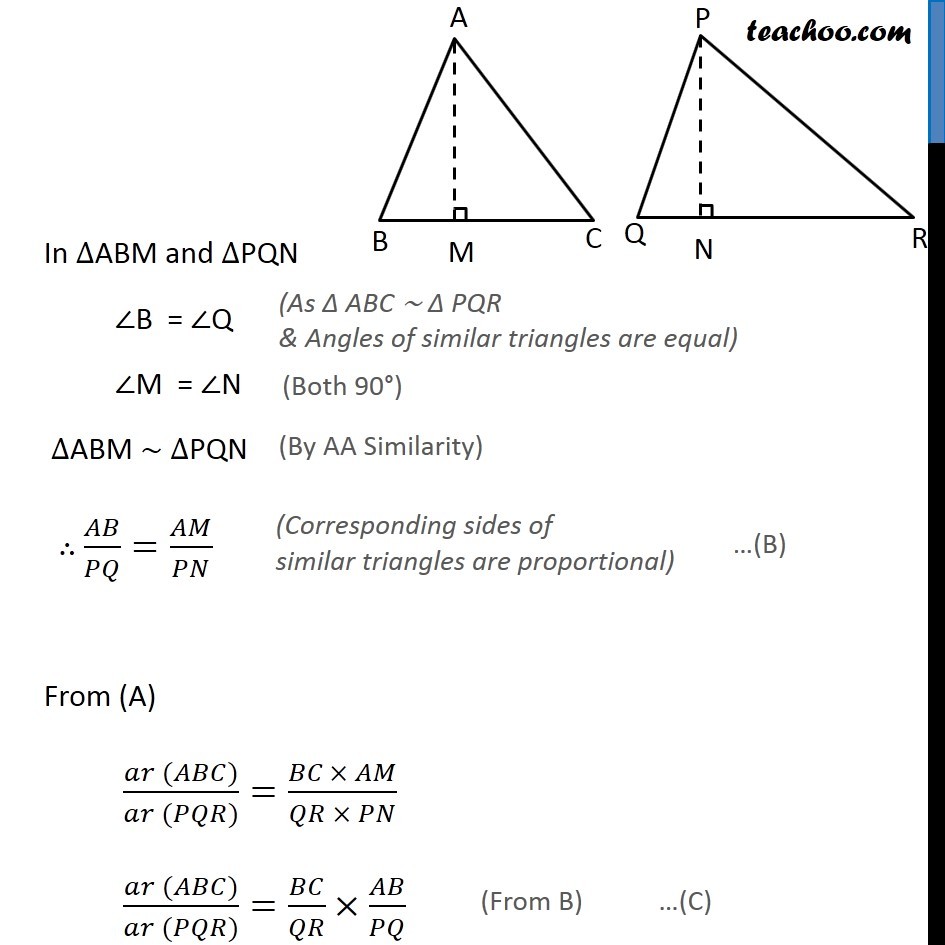
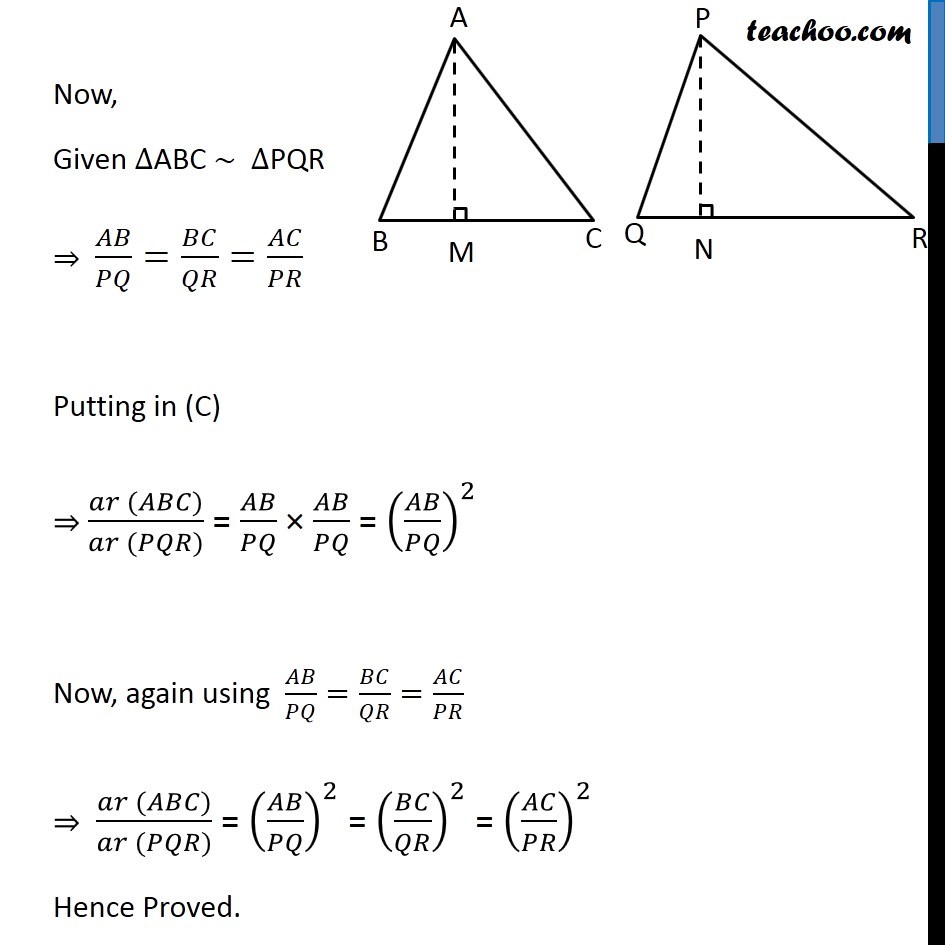
Theorem 6.6: The ratio of the areas of two similar triangles is equal to the square of ratio of their corresponding sides. Given: ∆ABC ~ ∆PQR To Prove: (𝑎𝑟 (𝐴𝐵𝐶))/(𝑎𝑟 (𝑃𝑄𝑅)) = (𝐴𝐵/𝑃𝑄)^2 = (𝐵𝐶/𝑄𝑅)^2 = (𝐴𝐶/𝑃𝑅)^2 Construction: Draw AM ⊥ BC and PN ⊥ QR. Proof: ar (ABC) = 1/2 × Base × Height = 1/2 × BC × AM ar (PQR) = 1/2 × Base × Height = 1/2 × QR × PN ar (PQR) = 1/2 × Base × Height = 1/2 × QR × PN In ∆ABM and ∆PQN ∠B = ∠Q ∠M = ∠N ∆ABM ∼ ∆PQN ∴ 𝐴𝐵/𝑃𝑄=𝐴𝑀/𝑃𝑁From (A) (𝑎𝑟 (𝐴𝐵𝐶))/(𝑎𝑟 (𝑃𝑄𝑅))=(𝐵𝐶\ × 𝐴𝑀)/(𝑄𝑅 × 𝑃𝑁) (𝑎𝑟 (𝐴𝐵𝐶))/(𝑎𝑟 (𝑃𝑄𝑅))=𝐵𝐶/𝑄𝑅 × 𝐴𝐵/𝑃𝑄 Now, Given ∆ABC ~ ∆PQR ⇒ 𝐴𝐵/𝑃𝑄=𝐵𝐶/𝑄𝑅=𝐴𝐶/𝑃𝑅 Putting in (C) ⇒ (𝑎𝑟 (𝐴𝐵𝐶))/(𝑎𝑟 (𝑃𝑄𝑅)) = 𝐴𝐵/𝑃𝑄 × 𝐴𝐵/𝑃𝑄 = (𝐴𝐵/𝑃𝑄)^2 Now, again using 𝐴𝐵/𝑃𝑄=𝐵𝐶/𝑄𝑅=𝐴𝐶/𝑃𝑅 ⇒ (𝑎𝑟 (𝐴𝐵𝐶))/(𝑎𝑟 (𝑃𝑄𝑅)) = (𝐴𝐵/𝑃𝑄)^2 = (𝐵𝐶/𝑄𝑅)^2 = (𝐴𝐶/𝑃𝑅)^2 Hence Proved.