Theorem 6.3 - Chapter 6 Class 10 Triangles

Transcript

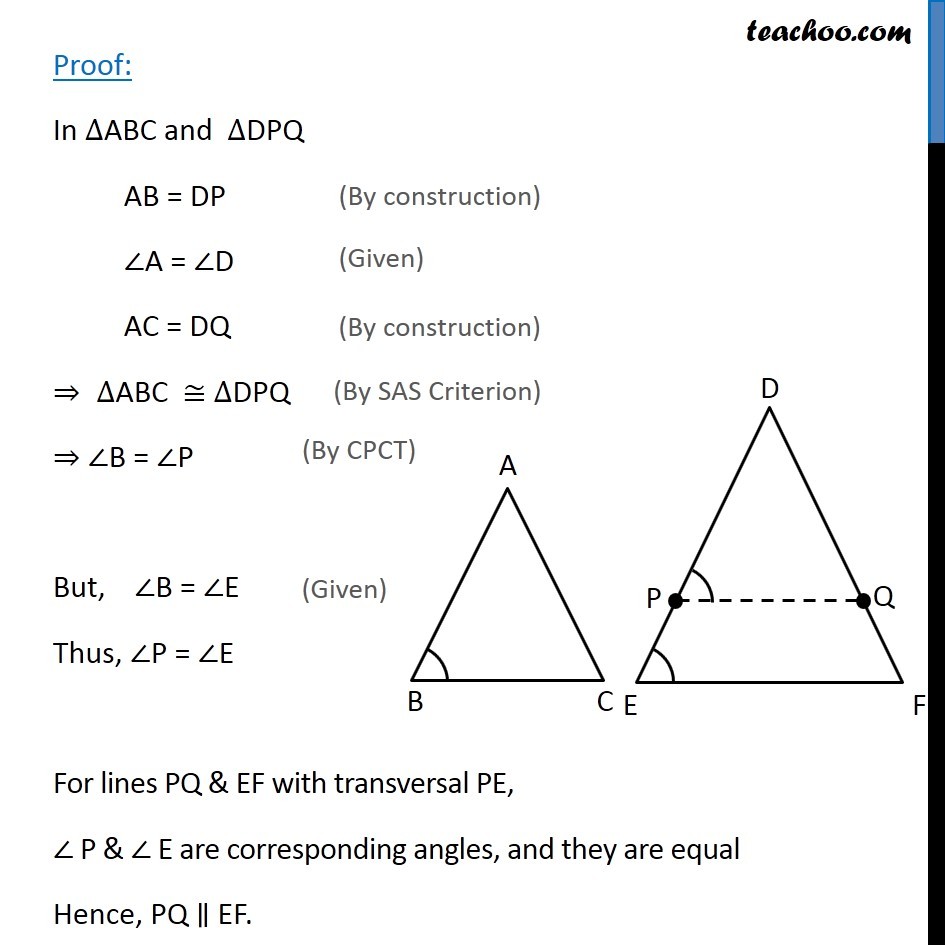
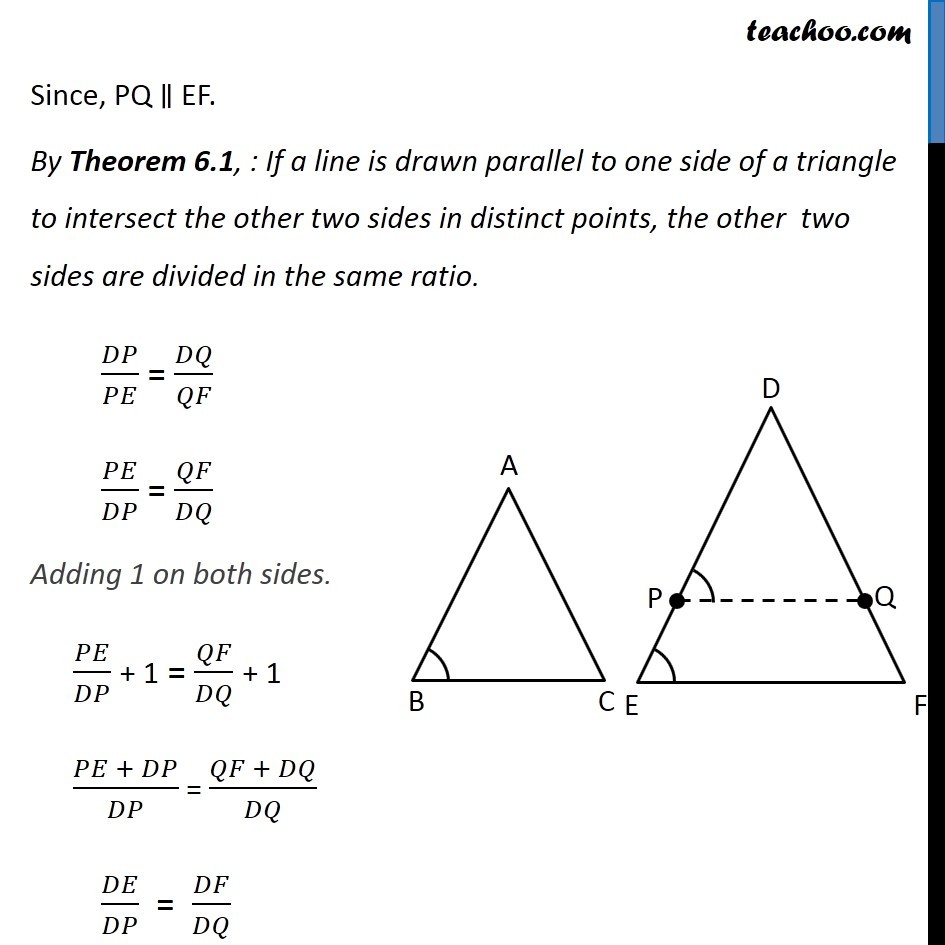
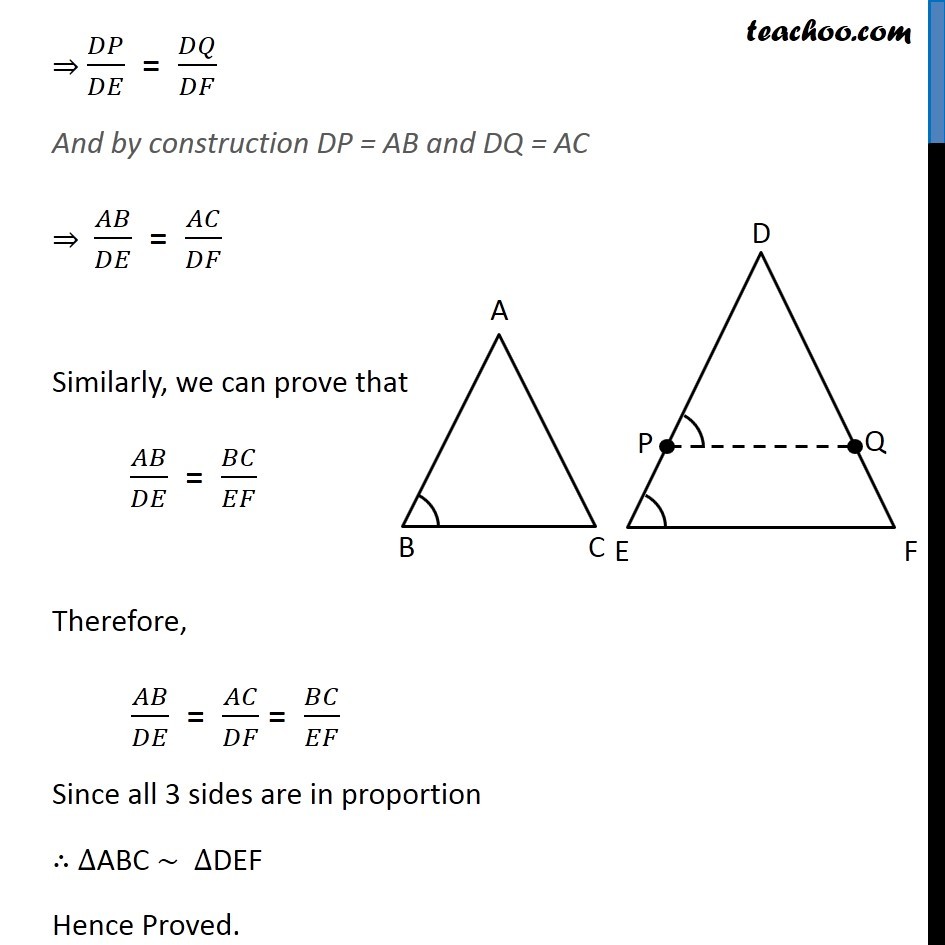
Theorem 6.3 (AAA Criteria) If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangle are similar.Given: Two triangles ∆ABC and ∆DEF such that ∠A = ∠D, ∠B = ∠E & ∠C = ∠F To Prove: ∆ABC ~ ∆DEF Construction: Draw P and Q on DE & DF such that DP = AB and DQ = AC respectively and join PQ. Proof: In ∆ABC and ∆DPQ AB = DP ∠A = ∠D AC = DQ ⇒ ∆ABC ≅ ∆DPQ ⇒ ∠B = ∠P But, ∠B = ∠E Thus, ∠P = ∠E For lines PQ & EF with transversal PE, ∠ P & ∠ E are corresponding angles, and they are equal Hence, PQ ∥ EF. Since, PQ ∥ EF. By Theorem 6.1, : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. 𝐷𝑃/𝑃𝐸 = 𝐷𝑄/𝑄𝐹 𝑃𝐸/𝐷𝑃 = 𝑄𝐹/𝐷𝑄 Adding 1 on both sides. 𝑃𝐸/𝐷𝑃 + 1 = 𝑄𝐹/𝐷𝑄 + 1 (𝑃𝐸 + 𝐷𝑃)/𝐷𝑃 = (𝑄𝐹 + 𝐷𝑄)/𝐷𝑄 𝐷𝐸/𝐷𝑃 = 𝐷𝐹/𝐷𝑄 ⇒ 𝐷𝑃/𝐷𝐸 = 𝐷𝑄/𝐷𝐹 And by construction DP = AB and DQ = AC ⇒ 𝐴𝐵/𝐷𝐸 = 𝐴𝐶/𝐷𝐹 Similarly, we can prove that 𝐴𝐵/𝐷𝐸 = 𝐵𝐶/𝐸𝐹 Therefore, 𝐴𝐵/𝐷𝐸 = 𝐴𝐶/𝐷𝐹 = 𝐵𝐶/𝐸𝐹 Since all 3 sides are in proportion ∴ ∆ABC ~ ∆DEF Hence Proved.