Check sibling questions

Theorem 8.9 - Chapter 8 Class 9 Quadrilaterals

Last updated at May 29, 2023 by

Theorem 8.10 - Line drawn through mid-point of one side of a triangle

Theorem 8.10 - Chapter 8 Class 9 Quadrilaterals - Part 2
Theorem 8.10 - Chapter 8 Class 9 Quadrilaterals - Part 3

This video is only available for Teachoo black users

Subscribe Now

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

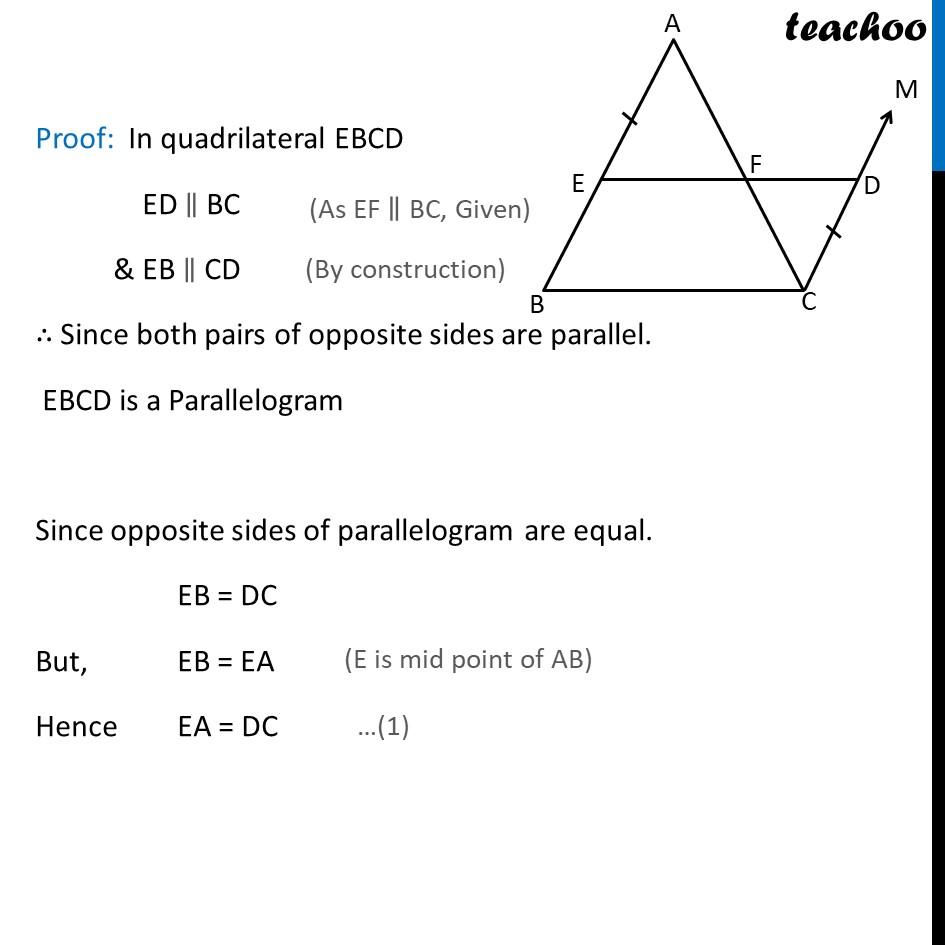
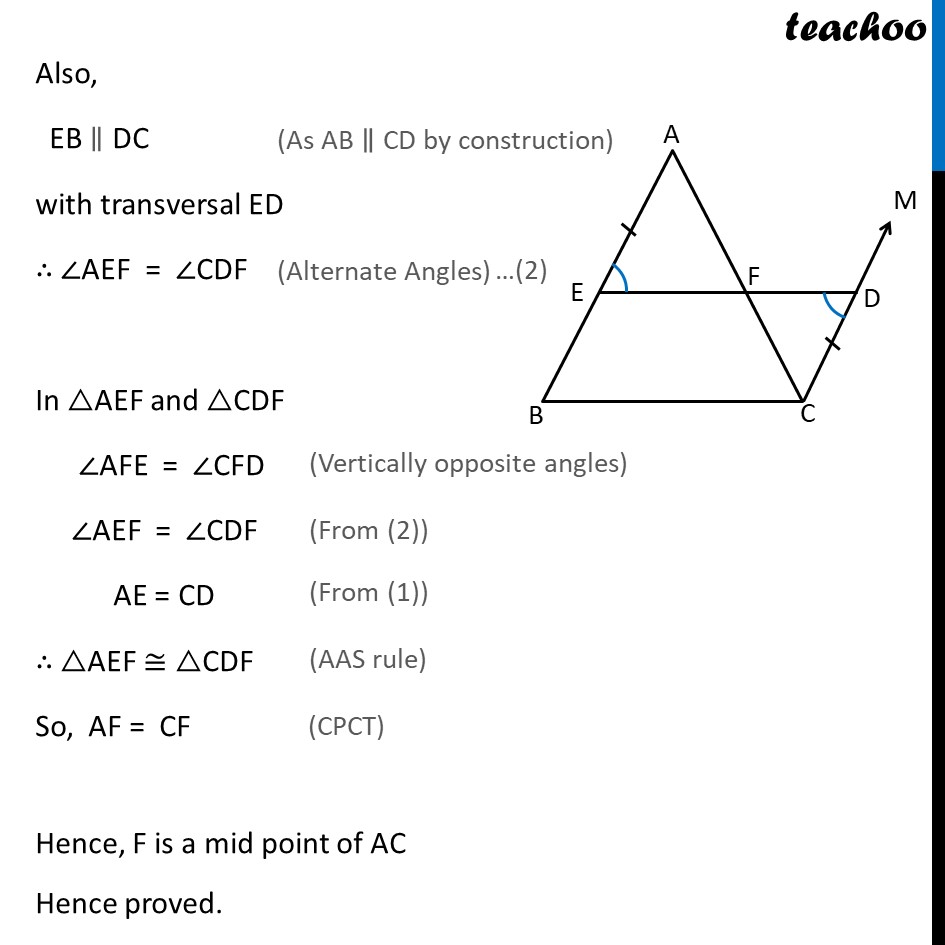
Theorem 8.10 The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side. Given : ABC where E is mid point of AB , F is some point on AC & EF BC To Prove : F is a mid point of AC. Construction : Through C draw CM AB Extend EF and let it cut CM at D. Proof: In quadrilateral EBCD ED BC & EB CD Since both pairs of opposite sides are parallel. EBCD is a Parallelogram Since opposite sides of parallelogram are equal. EB = DC But, EB = EA Hence EA = DC Also, EB DC with transversal ED AEF = CDF In AEF and CDF AEF = CDF AFE = CFD AE = CD AEF CDF So, AF = CD Hence, F is a mid point of AC Hence proved.

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.