Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class
Theorem 8.8 - Chapter 8 Class 9 Quadrilaterals
Last updated at May 29, 2023 by Teachoo
Transcript
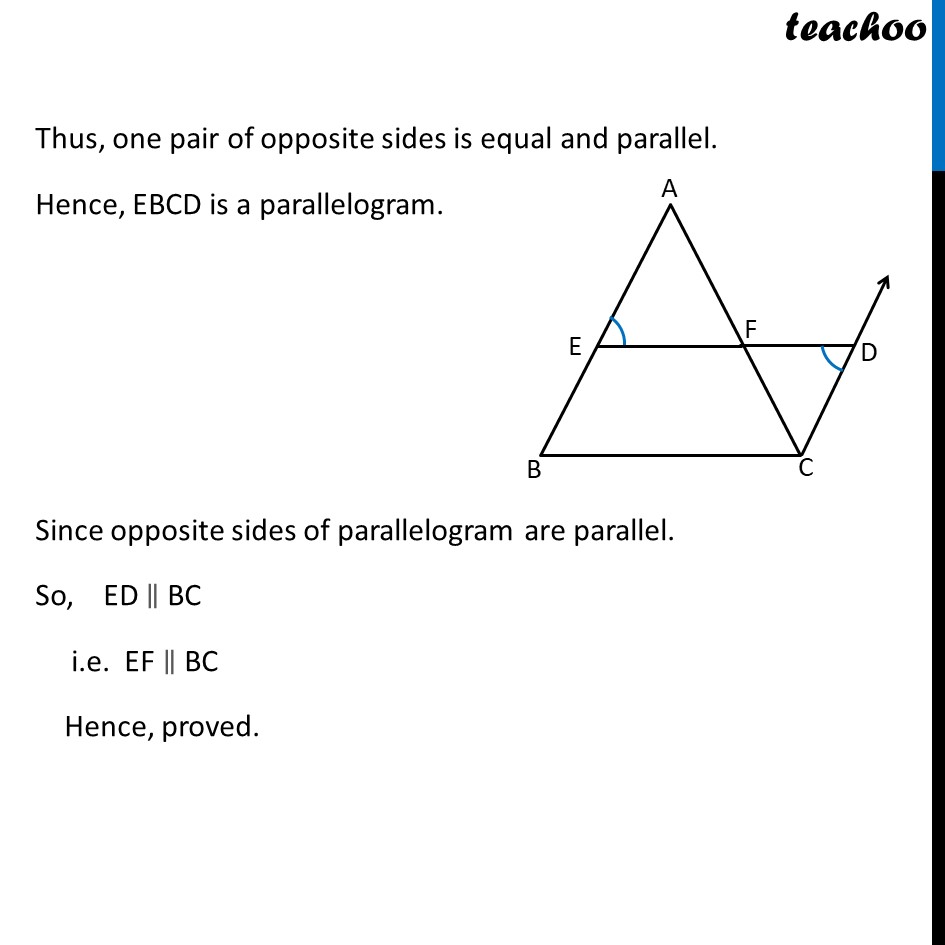
Theorem 8.9 The line segment joining the mid-points of two sides of a triangle is parallel to the third side. Given : ABCD is a triangle where E and F are mid points of AB and AC respectively To Prove : EF BC Construction : Through C draw a line segment parallel to AB & extend EF to meet this line at D. Proof : Since EB DC with transversal ED. AEF = CDF In AEF and CDF AEF = CDF AF = CF AFE = CFD AEF CDF So, EA = DC But, EA = EB Hence, EB = DC Now, In EBCD, EB DC & EB = DC Thus, one pair of opposite sides is equal and parallel. Hence EBCD is a parallelogram. Since opposite sides of parallelogram are parallel. So, ED BC i.e. EF BC Hence, proved.
