
Side inequality
Last updated at December 16, 2024 by Teachoo



Transcript
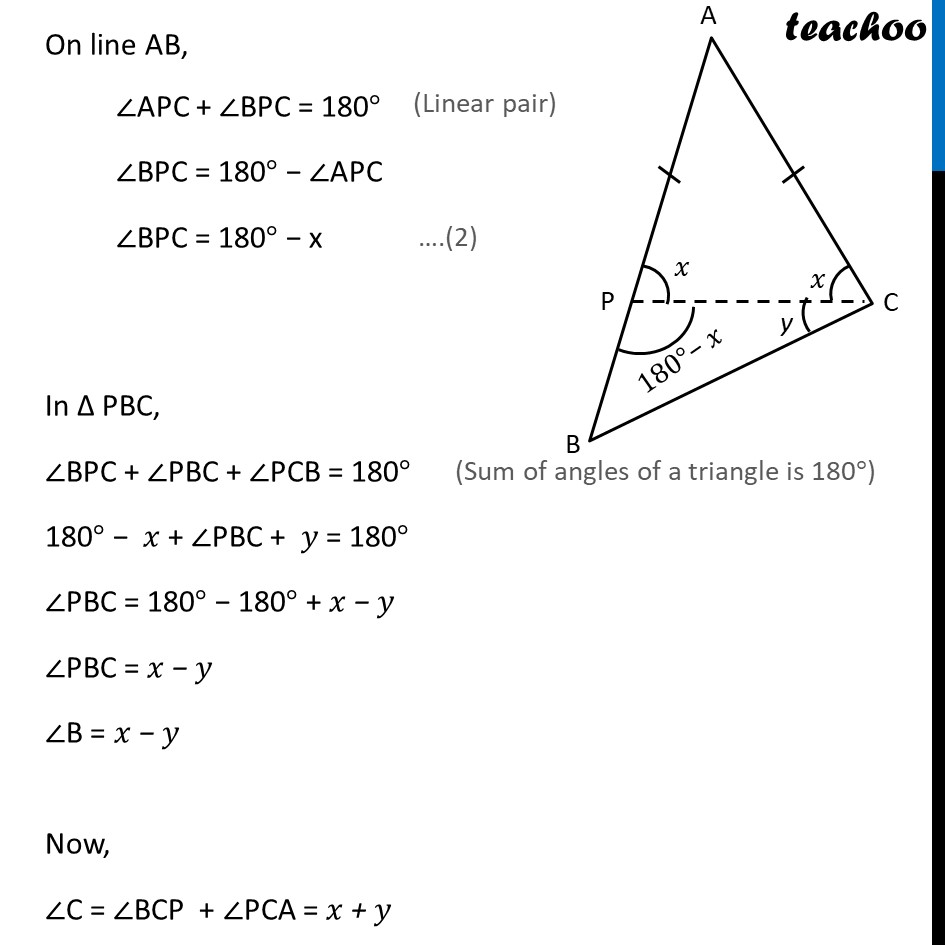
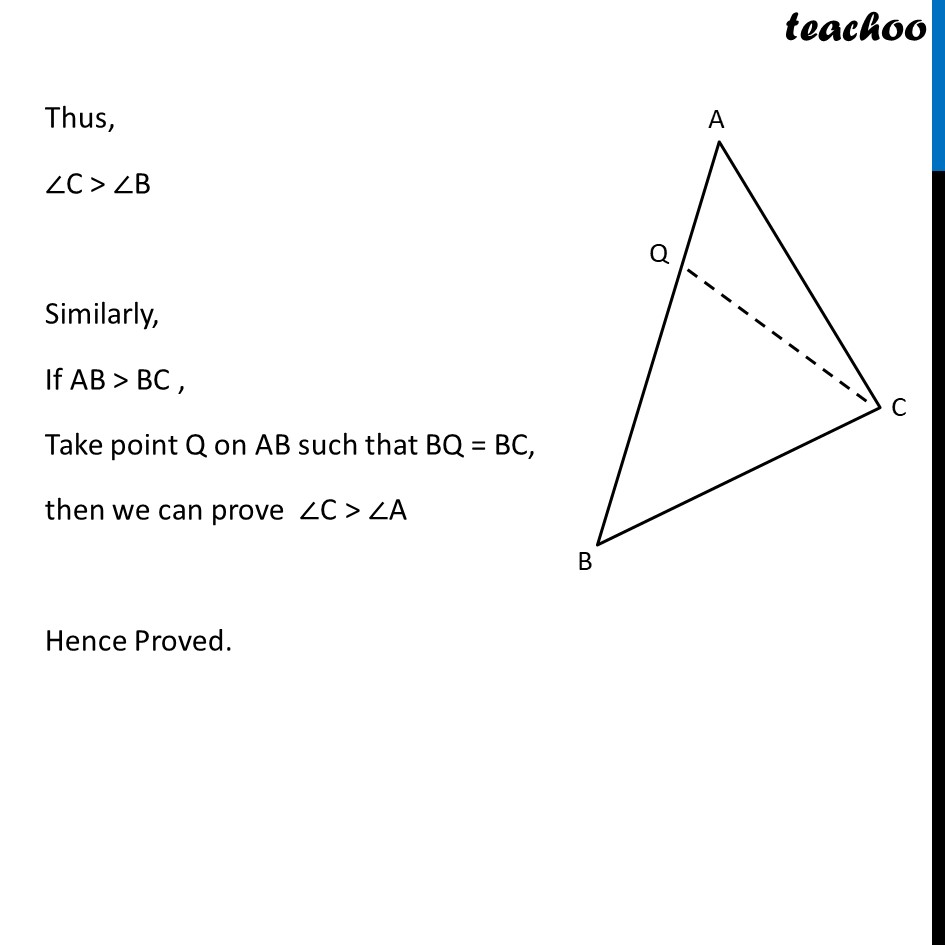
Theorem 7.6 :- If two sides of a triangle are unequal, the angle opposite to larger side is larger ( or greater ). Given :- ∆ABC such that AB > AC . To Prove :- ∠C > ∠B . Construction:- Take a point P on AB such that AP = AC and join CP. Let ∠APC = x° & ∠BCP = y° Proof:- Since AP = AC ⇒ ∠ACP = ∠APC ⇒ ∠ACP = x On line AB, ∠APC + ∠BPC = 180° ∠BPC = 180° − ∠APC ∠BPC = 180° − x In Δ PBC, ∠BPC + ∠PBC + ∠PCB = 180° 180° − 𝑥 + ∠PBC + 𝑦 = 180° ∠PBC = 180° − 180° + 𝑥 − 𝑦 ∠PBC = 𝑥 − 𝑦 ∠B = 𝑥 − 𝑦 Now, ∠C = ∠BPC + ∠PCA = 𝑥 + 𝑦 Thus, ∠C > ∠B Similarly, If AB > BC , Take point Q on AB such that BQ = BC, then we can prove ∠C > ∠A Hence Proved.