

Bayes theorem
Bayes theorem
Last updated at December 16, 2024 by Teachoo



Transcript
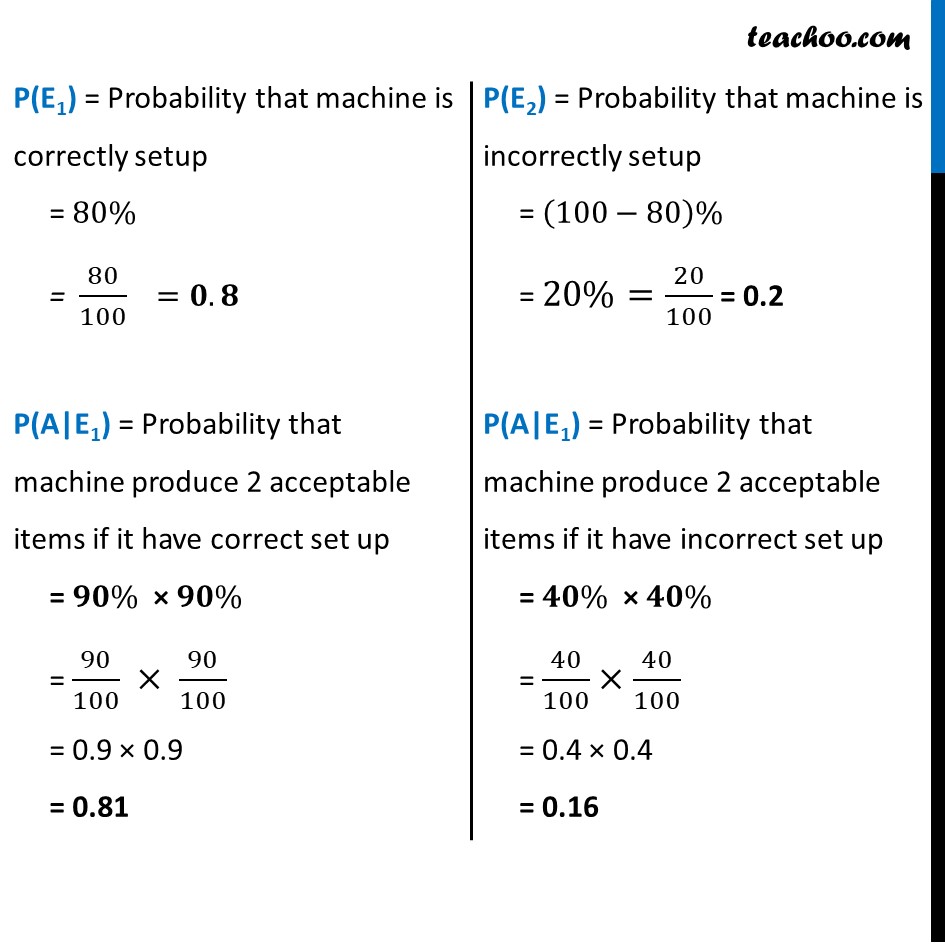
Example 24 If a machine is correctly set up, it produces 90% acceptable items. If it is incorrectly set up, it produces only 40% acceptable items. Past experience shows that 80% of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly setup.Let E1 : Event that the machine is correctly setup E2 : Event that the machine is incorrectly setup A : Event that the Machine produce two acceptable items We need to find out the probability that the machine have a correct set up if it produce two acceptable item i.e. P(E1|A) P(E1|A) = (𝑃(𝐸_1 ).𝑃(𝐴|𝐸_1))/(𝑃(𝐸_1 ).𝑃(𝐴|𝐸_1)+𝑃(𝐸_2 ).𝑃(𝐴|𝐸_2) ) "P(E1)" = Probability that machine is correctly setup = 80% = 80/100 =𝟎.𝟖 P(A|E1) = Probability that machine produce 2 acceptable items if it have correct set up = 𝟗𝟎% × 𝟗𝟎% = 90/100 × 90/100 = 0.9 × 0.9 = 0.81 "P(E1)" = Probability that machine is correctly setup = 80% = 80/100 =𝟎.𝟖 P(A|E1) = Probability that machine produce 2 acceptable items if it have correct set up = 𝟗𝟎% × 𝟗𝟎% = 90/100 × 90/100 = 0.9 × 0.9 = 0.81 "P(E2)" = Probability that machine is incorrectly setup = (100−80)% = 20%=20/100 = 0.2 P(A|E1) = Probability that machine produce 2 acceptable items if it have incorrect set up = 𝟒𝟎% × 𝟒𝟎% = 40/100×40/100 = 0.4 × 0.4 = 0.16 Putting values in the formula P(E1|A) = (𝑃(𝐸_1 ).𝑃(𝐴|𝐸_1))/(𝑃(𝐸_1 ).𝑃(𝐴|𝐸_1)+𝑃(𝐸_2 ).𝑃(𝐴|𝐸_2) ) = (0.8 × 𝟎.𝟖𝟏)/(0.8 × 𝟎.𝟖𝟏 + 0.2 × 𝟎.𝟏𝟔) = 0.648/0.680 = 0.95