Example 33 - Chapter 13 Class 12 Probability (Term 2)

Transcript

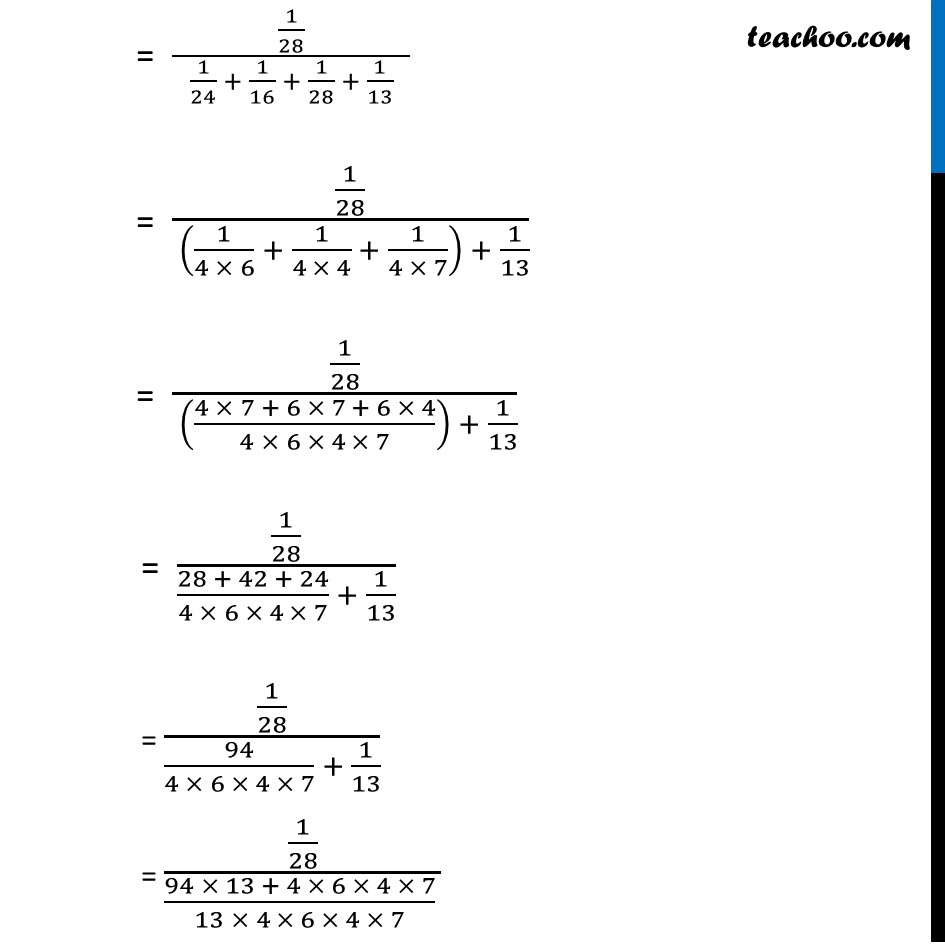
Example 33 Coloured balls are distributed in four boxes as shown in the following table: A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black, what is the probability that ball drawn is from the boxs III?Let A : Event that a black ball is selected E1 : Event that the ball is selected from box I E2 : Event that the ball is selected from box II E3 : Event that the ball is selected from box III E4 : Event that the ball is selected from box IV We need to find out the Probability of the ball drawn is from box III if it is black. i.e. P(E3|A) P(E3|A)= (𝑃(𝐸3).𝑃(𝐴|𝐸3))/(𝑃(𝐸1)𝑃(𝐴|𝐸1)+𝑃(𝐸2)𝑃(𝐴|𝐸2)+𝑃(𝐸3)𝑃(𝐴|𝐸3)+𝑃(𝐸4)𝑃(𝐴|𝐸4)) P(E1) = Probability that ball drawn is from box I = 1/4 P(A|E1) = Probability of that black ball is selected from Box I = (𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠)/(𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑏𝑜𝑥) = 3/18 P(E2) = Probability that ball drawn is from box II = 1/4 P(A|E2) = Probability of that black ball is selected from Box II = (𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠)/(𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑏𝑜𝑥) = 2/8 = 1/4 P(E3) = Probability that ball drawn is from box III = 1/4 P(A|E3) = Probability of that black ball is selected froAm Box II = (𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠)/(𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑏𝑜𝑥) = 1/7 P(E4) = Probability that ball drawn is from box IV = 1/4 P(A|E4) = Probability of that black ball is selected from Box IV = (𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠)/(𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑙𝑙𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑏𝑜𝑥) = 4/13 Putting values in Equation "P(E3|A)"=(𝑃(𝐸3).𝑃(𝐴|𝐸3))/(𝑃(𝐸1)𝑃(𝐴|𝐸1)+𝑃(𝐸2)𝑃(𝐴|𝐸2)+𝑃(𝐸3)𝑃(𝐴|𝐸3)+𝑃(𝐸4)𝑃(𝐴|𝐸4)) = (1/4 × 1/7)/( 1/4 × 3/18 + 1/4 × 1/4 + 1/4 × 1/7 + 1/4 × 4/13 ) = (1/28)/( 1/24 + 1/16 + 1/28 + 1/13 ) = (1/28)/( (1/(4 × 6) + 1/(4 × 4) + 1/(4 × 7)) + 1/13) = (1/28)/( ((4 × 7 + 6 × 7 + 6 × 4)/(4 × 6 × 4 × 7)) + 1/13) = (1/28)/((28 + 42 + 24)/(4 × 6 × 4 × 7) + 1/13) = (1/28)/(94/(4 × 6 × 4 × 7) + 1/13) = (1/28)/((94 × 13 + 4 × 6 × 4 × 7)/(13 × 4 × 6 × 4 × 7) ) = 1/((94 × 13 + 4 × 6 × 4 × 7)/(13 × 4 × 6) ) = (13 × 4 × 6)/( 94 × 13 + 4 × 6 × 4 × 7) = (13 × 2 × 6)/( 47 × 13 + 2 × 6 × 4 × 7) = 156/(611 + 336) = 156/947 = 0.164