Example 17 - Chapter 13 Class 12 Probability

Transcript

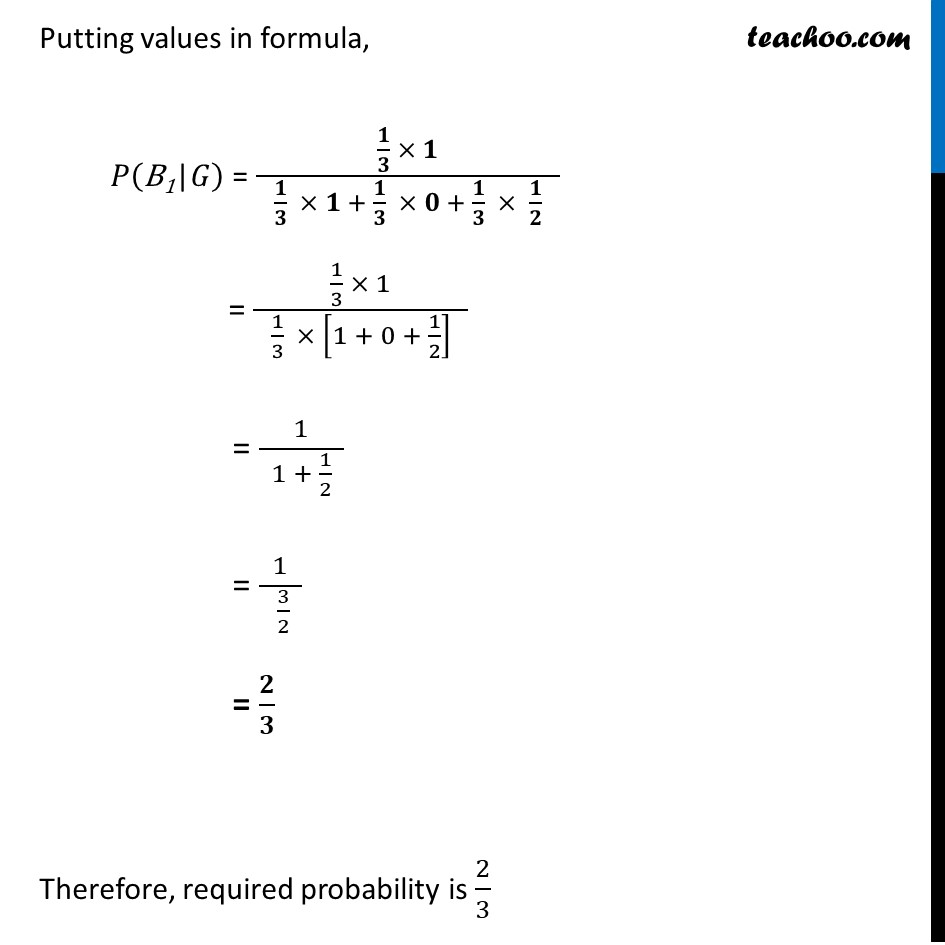
Example 17 Given three identical boxes I, II and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in the box III, there is one gold and one silver coin. A person chooses a box at coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold?Let B1 : Selecting Box 1 having two gold coins B2 : Selecting Box 2 having two silver coins B3 : Selecting Box 3 having one gold and one silver coin G : The second coin is of gold We need to find the Probability that the other coin in the box is also of gold, if the first coin is of gold i.e. P(B1"|"G) P(B1"|"G) = (𝑃(𝐵_1 ).𝑃(𝐺|𝐵_1))/(𝑃(𝐵_1 ).𝑃(𝐺|𝐵_1)+𝑃(𝐵_2 ).𝑃(𝐺|𝐵_2)+𝑃(𝐵_3 ).𝑃(𝐺|𝐵_3)) "P(B1)" = Probability of selecting Box 1 = 𝟏/𝟑 𝑷(𝑮"|B1") = Probability that second coin is of gold in Box 1 = 𝟏 "P(B2)" = Probability of selecting Box 2 = 𝟏/𝟑 𝑷(𝑮"|B2") = Probability that second coin is of gold in Box 2 = 𝟎 "P(B3)" = Probability of selecting Box 3 = 𝟏/𝟑 𝑷(𝑮"|B3") = Probability that second coin is of gold in Box 3 = 𝟏/𝟐 Putting values in formula, 𝑃("B1|" 𝐺) = (𝟏/𝟑 × 𝟏)/( 𝟏/𝟑 × 𝟏 + 𝟏/𝟑 × 𝟎 + 𝟏/𝟑 × 𝟏/𝟐 ) = (1/3 × 1)/( 1/3 × [1 + 0 + 1/2] ) = 1/( 1 + 1/2 ) = 1/( 3/2 ) = 𝟐/𝟑 Therefore, required probability is 2/3