Example 16 - Chapter 13 Class 12 Probability

Transcript

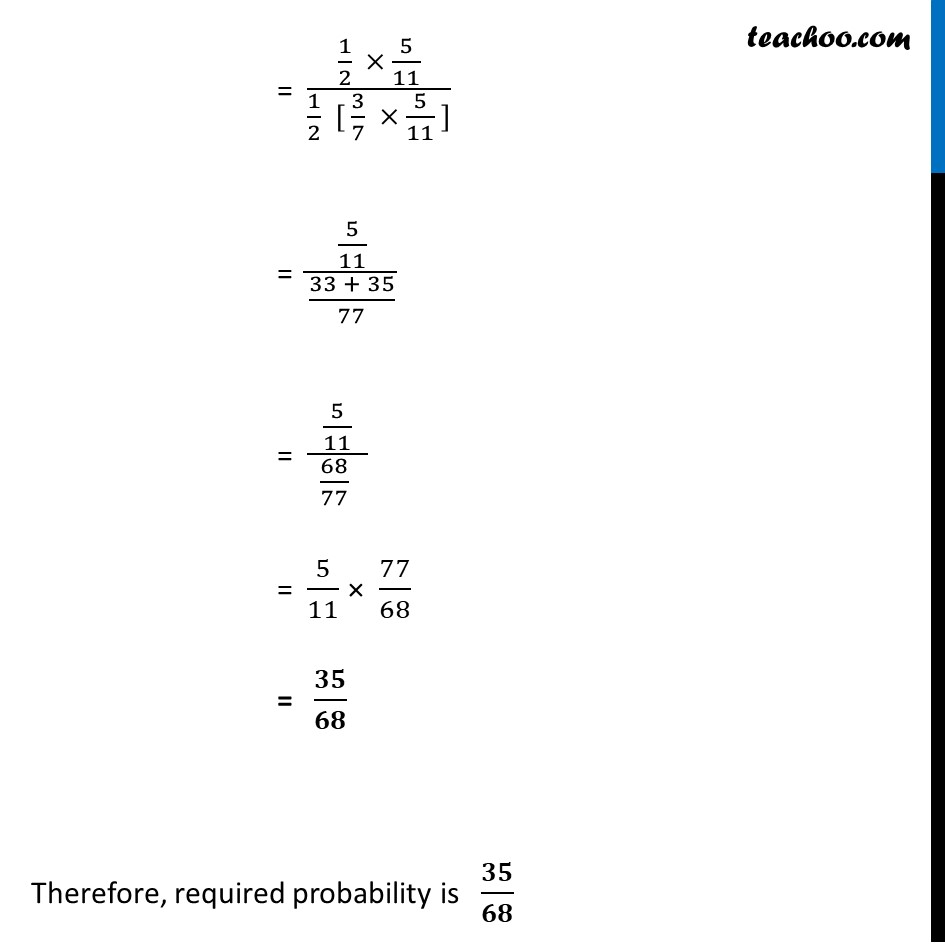
Example 16 Bag I contains 3 red & 4 black balls while another Bag II contains 5 red & 6 black balls. One ball is drawn at random from one of bags & it is found to be red. Find the probability that it was drawn from Bag II. Let E1 : Bag selected is bag 1 E2 : Bag selected is bag 2 A : Ball selected is Red B : Ball selected is Black We need to find P(ball was drawn from bag 2, if ball is red) = P(E2|A) We need to find, 𝑷(𝑬𝟐"|" 𝑨)=(𝑷(𝑨) 𝑷(𝑨"|" 𝑬𝟐))/(𝑷(𝑬𝟏) 𝑷(𝑨"|" 𝑬𝟏) + 𝑷(𝑬𝟐) 𝑷(𝑨"|" 𝑬𝟐)) "P(E1)" = Probability bag selected is Bag I = 𝟏/𝟐 "P(E2)" = Probability bag selected is Bag II = 𝟏/𝟐 "P(A|E2)" = Probability red ball was selected from Bag II = 5/(5 + 6) = 𝟓/𝟏𝟏 "P(A|E1)" = Probability red ball was selected from Bag I = 3/(3 + 4) = 𝟑/𝟕 Putting values in formula, P("E2|"A) = (𝟏/𝟐 × 𝟓/𝟏𝟏)/( 𝟏/𝟐 × 𝟑/𝟕 + 𝟏/𝟐 × 𝟓/𝟏𝟏 ) = (1/2 × 5/11)/(1/2 [ 3/7 × 5/11 ]) = (5/11)/((33 + 35)/77) = (5/11)/( 68/77 ) = 5/11 × 77/68 = 𝟑𝟓/𝟔𝟖 Therefore, required probability is 𝟑𝟓/𝟔𝟖 = (1/2 × 5/11)/(1/2 [ 3/7 × 5/11 ]) = (5/11)/((33 + 35)/77) = (5/11)/( 68/77 ) = 5/11 × 77/68 = 𝟑𝟓/𝟔𝟖 Therefore, required probability is 𝟑𝟓/𝟔𝟖