Ex 13.2, 14 - Chapter 13 Class 12 Probability

Transcript

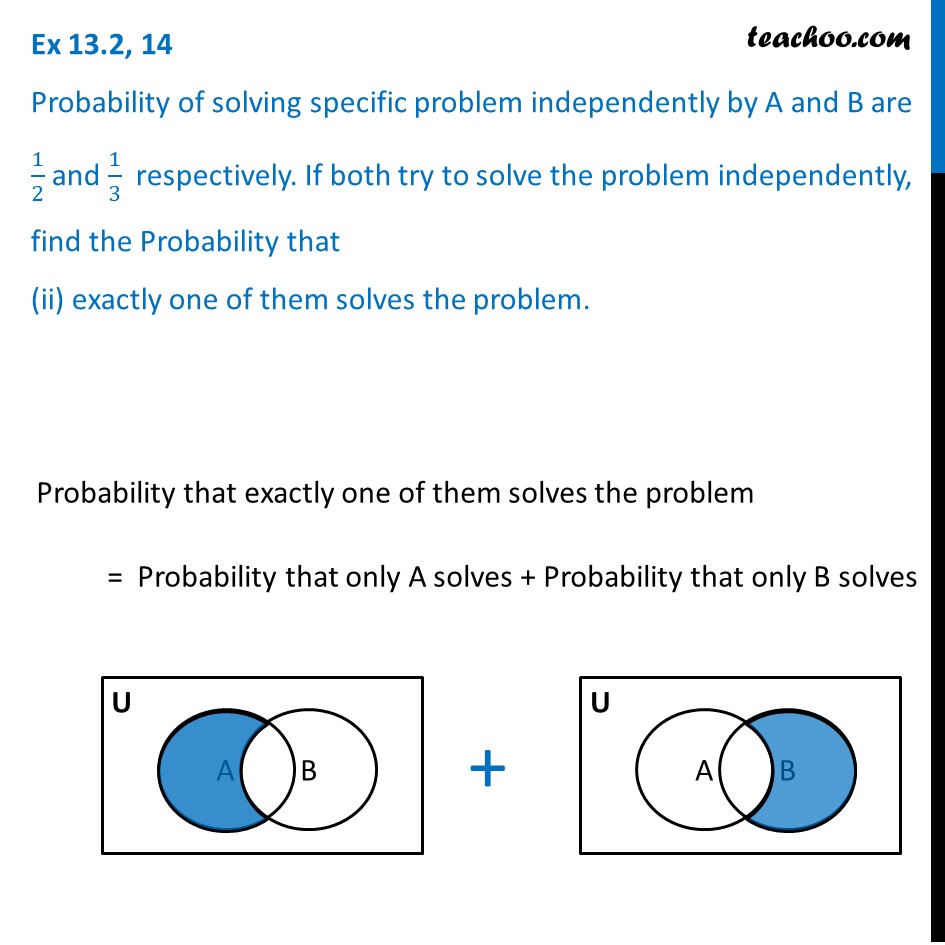
Ex 13.2, 14 Probability of solving specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem independently, find the Probability that (i) the problem is solved.Given, P(A) = 1/2 & P(B) = 1/3 Probability that the problem is solved = Probability that A solves the problem or B solves the problem = P(A ∪ B) = P(A) + P(B) – P(A ∩ B) Since A & B are independent, P(A ∩ B) = P(A) . P(B) = 1/2 × 1/3 = 1/6 Now, P(Problem is solved) = P(A) + P(B) – P(A ∩ B) = 1/2 + 1/3 – 1/6 = 3/6 + 2/6 – 1/6 = 4/6 = 𝟐/𝟑 Ex 13.2, 14 Probability of solving specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem independently, find the Probability that (ii) exactly one of them solves the problem. Probability that exactly one of them solves the problem = Probability that only A solves + Probability that only B solves Therefore, P(exactly one of them solves) = P(A alone solves) + P(B alone solves) = P(A ∩ B’) + P(B ∩ A’) = (P(A) – P(A ∩ B)) + (P(B) – P(B ∩ A)) = P(A) + P(B) – 2P(A ∩ B) = 1/2 + 1/3 – 2 × 1/6 = 1/2 + 1/3 – 1/3 = 𝟏/𝟐