You are here
Question 9 - Composite functions - Chapter 1 Class 12 Relation and Functions
Last updated at Dec. 16, 2024 by Teachoo
Chapter 1 Class 12 Relation and Functions
Concept wise
- Relations - Definition
- Empty and Universal Relation
- To prove relation reflexive, transitive, symmetric and equivalent
- Finding number of relations
- Function - Definition
- To prove one-one & onto (injective, surjective, bijective)
-
Composite functions
- Composite functions and one-one onto
- Finding Inverse
- Inverse of function: Proof questions
- Binary Operations - Definition
- Whether binary commutative/associative or not
- Binary operations: Identity element
- Binary operations: Inverse
Transcript
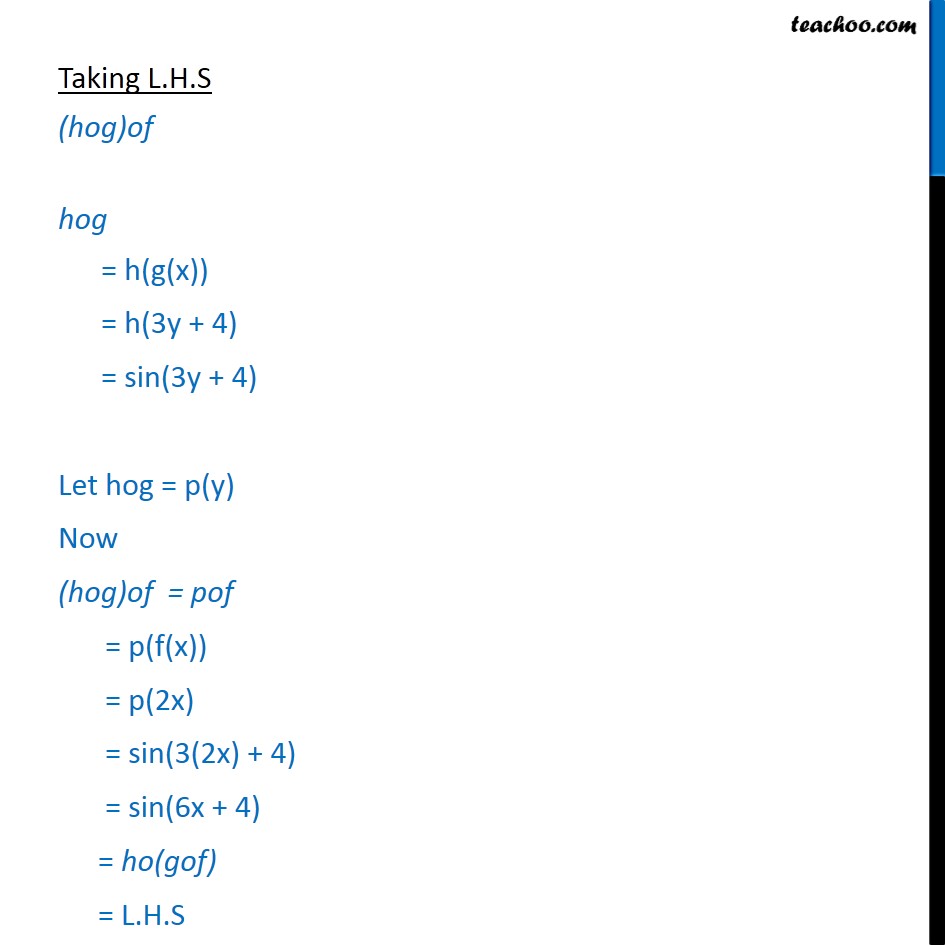
Question 9 Consider f : N → N, g : N → N and h : N → R defined as f (x) = 2x, g (y) = 3y + 4 and h (z) = sin z, ∀ x, y and z in N. Show that ho(gof) = (hog)of. f(x) = 2x , g(y) = 3y + 4 & h(z) = sin z We have to prove ho(gof) = (hog)of Taking L.H.S ho(gof) gof = g(f(x)) = g(2x) = 3(2x) + 4 = 6x + 4 ho(gof) = h(6x + 4) = sin(6x + 4) Taking L.H.S (hog)of hog = h(g(x)) = h(3y + 4) = sin(3y + 4) Let hog = p(y) Now (hog)of = pof = p(f(x)) = p(2x) = sin(3(2x) + 4) = sin(6x + 4) = ho(gof) = L.H.S Since L.H.S = R.H.S Hence proved
