Question 16 - Miscellaneous - Chapter 11 Class 12 Three Dimensional Geometry

Transcript

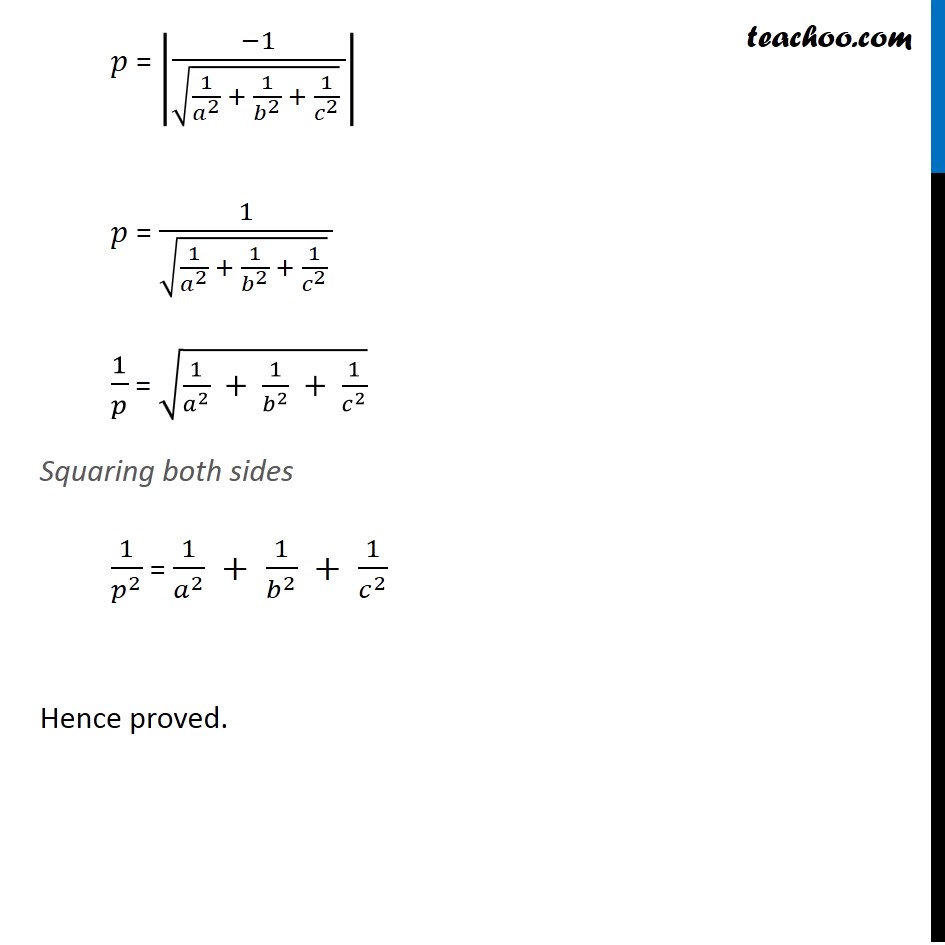
Question 16 Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then 1/𝑎2 + 1/𝑏2 + 1/𝑐2 = 1/𝑝2 . Distance of the point (𝑥_1,𝑦_1,𝑧_1) from the plane Ax + By + Cz = D is |(𝑨𝒙_𝟏 + 𝑩𝒚_𝟏 + 𝑪𝒛_𝟏 − 𝑫)/√(𝑨^𝟐 + 𝑩^𝟐 + 𝑪^𝟐 )| The equation of a plane having intercepts 𝑎, b, c on the x −, y − & z − axis respectively is 𝒙/𝒂 + 𝒚/𝒃 + 𝒛/𝒄 = 1 Comparing with Ax + By + Cz = D, A = 1/𝑎 , B = 1/𝑏 , C = 1/𝑐 , D = 1 Given, the plane is at a distance of ‘𝑝’ units from the origin. So, The point is O(0, 0, 0) So, 𝑥_1 = 0, 𝑦_1= 0, 𝑧_1= 0 Now, Distance = |(𝐴𝑥_1 + 𝐵𝑦_1 + 𝐶𝑧_1 − 𝐷)/√(𝐴^2 + 𝐵^2 + 𝐶^2 )| Putting values 𝑝 = |(1/𝑎 × 0 + 1/𝑏 × 0 + 1/𝑐 × 0 − 1)/√((1/𝑎)^2+ (1/𝑏)^2+ (1/𝑐)^2 )| 𝑝 = |(0 + 0 + 0 − 1)/(√(1/𝑎^2 + 1/𝑏^2 + 1/𝑐^2 ) )| 𝑝 = |(−1)/(√(1/𝑎^2 + 1/𝑏^2 + 1/𝑐^2 ) )| 𝑝 = 1/(√(1/𝑎^2 + 1/𝑏^2 + 1/𝑐^2 ) ) 1/𝑝 = √(1/𝑎^2 + 1/𝑏^2 + 1/𝑐^2 ) Squaring both sides 1/𝑝^2 = 1/𝑎^2 + 1/𝑏^2 + 1/𝑐^2 Hence proved.