Question 3 - Miscellaneous - Chapter 11 Class 12 Three Dimensional Geometry

Transcript

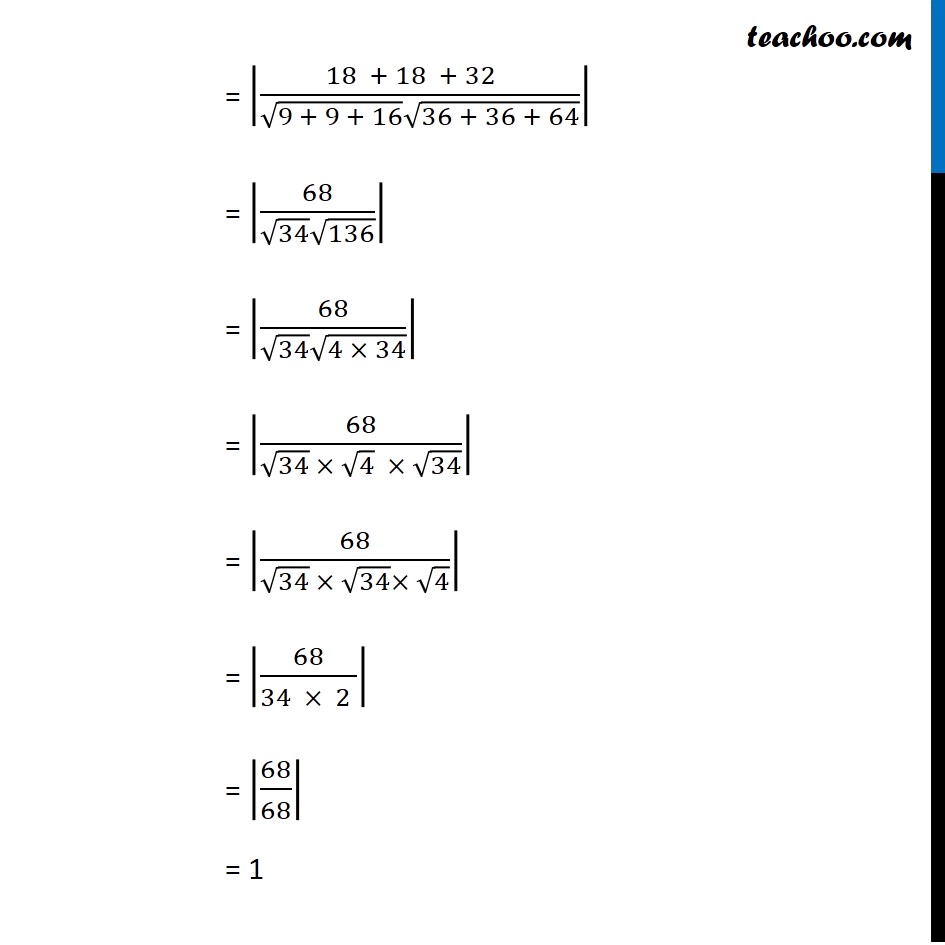
Question 3 If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (– 4, 3, – 6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.Angle between a pair of lines having direction ratios 𝑎1, 𝑏1, c1 and 𝑎_2 , 𝑏_2, 𝑐_2 is given by cos θ = |(𝒂_𝟏 𝒂_𝟐 + 𝒃_𝟏 𝒃_𝟐 + 𝒄𝟏𝒄𝟐)/(√(〖𝒂_𝟏〗^𝟐 + 〖𝒃_𝟏〗^𝟐+〖 𝒄_𝟏〗^𝟐 ) √(〖𝒂_𝟐〗^𝟐 + 〖𝒃_𝟐〗^𝟐+〖 𝒄_𝟐〗^𝟐 ))| A line passing through A (𝑥_1, 𝑦_1, 𝑧_1) and B (𝑥_2, 𝑦_2, 𝑧_2) has direction ratios (𝑥_2 − 𝑥_1), (𝑦_2 − 𝑦_1), (𝑧_2 − 𝑧_1) AB A (1, 2, 3) , B (4, 5, 7) Direction ratios of AB (4 − 1), (5 − 2),(7 − 3) = 3, 3, 4 ∴ 𝒂1 = 3, 𝒃1 = 3, 𝒄1 = 4 CD C (−4, 3, −6) ,D (2, 9, 2) Direction ratios of CD (2 − (–4)), (9 − 3),(2 – (–6)) = 6, 6, 8 ∴ 𝒂2 = 6, 𝒃2 = 6, 𝒄2 = 8 Now, cos θ = |(𝑎_1 𝑎_2 + 𝑏_1 𝑏_2 + 𝑐1𝑐2)/(√(〖𝑎_1〗^2 + 〖𝑏_1〗^2+〖 𝑐_1〗^2 ) √(〖𝑎_2〗^2 + 〖𝑏_2〗^2+〖 𝑐_2〗^2 ))| cos θ = |(3 × 6 + 3 × 6 + 4 × 8 )/(√(32 + 32 + 42) √(62 + 62 + 82))| = |(18 + 18 + 32 )/(√(9 + 9 + 16) √(36 + 36 + 64))| = |68/(√34 √136)| = |68/(√34 √(4 × 34))| = |68/(√34 × √4 × √34)| = |68/(√34 × √34× √4)| = |68/(34 × 2 )| = |68/68| = 1 ∴ cos θ = 1 So, θ = 0° Therefore, angle between AB and CD is 0° .