Misc 9 - Chapter 10 Class 12 Vector Algebra

Transcript

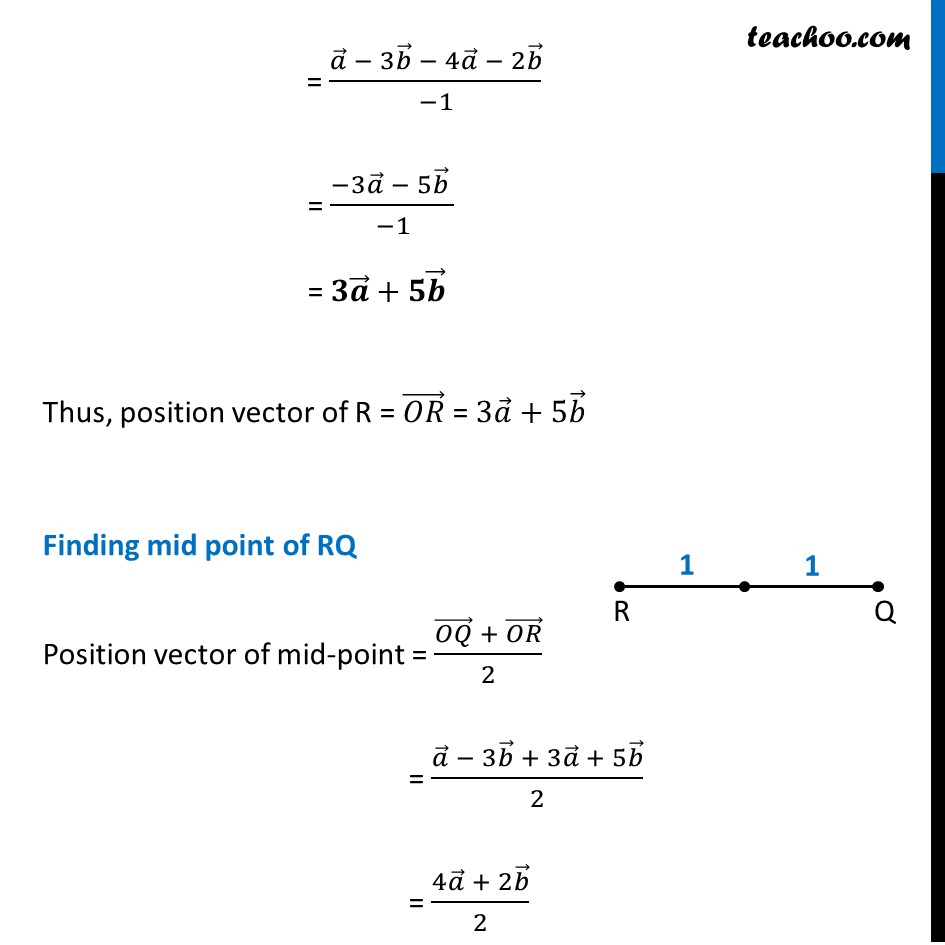
Misc 9 Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are (2𝑎 ⃗ + 𝑏 ⃗) and (𝑎 ⃗ – 3𝑏 ⃗) externally in the ratio 1 : 2. Also, show that P is the mid point of the line segment RQ. Given (𝑂𝑃) ⃗ = 2𝑎 ⃗ + 𝑏 ⃗ (𝑂𝑄) ⃗ = 𝑎 ⃗ − 3𝑏 ⃗ Since R divides PQ externally in the ratio 1 : 2 Position vector of R = (𝟏 × (𝑶𝑸) ⃗ − 𝟐 × (𝑶𝑷) ⃗)/(𝟏 − 𝟐) (𝑂𝑅) ⃗ = (1(𝑎 ⃗ − 3𝑏 ⃗ ) − 2(2𝑎 ⃗ + 𝑏 ⃗))/(−1) = (𝑎 ⃗ − 3𝑏 ⃗ − 4𝑎 ⃗ − 2𝑏 ⃗)/(−1) = (−3𝑎 ⃗ − 5𝑏 ⃗ )/(−1) = 𝟑𝒂 ⃗+𝟓𝒃 ⃗ Thus, position vector of R = (𝑂𝑅) ⃗ = 3𝑎 ⃗+5𝑏 ⃗ Finding mid point of RQ Position vector of mid-point = ((𝑂𝑄) ⃗ + (𝑂𝑅) ⃗)/2 = (𝑎 ⃗ − 3𝑏 ⃗ + 3𝑎 ⃗ + 5𝑏 ⃗)/2 = (4𝑎 ⃗ + 2𝑏 ⃗)/2 = 2𝑎 ⃗+𝑏 ⃗ This is the position vector of P. Thus, P is the mid point of RQ. Hence proved