
Addition(resultant) of vectors
Addition(resultant) of vectors
Last updated at December 16, 2024 by Teachoo



Transcript
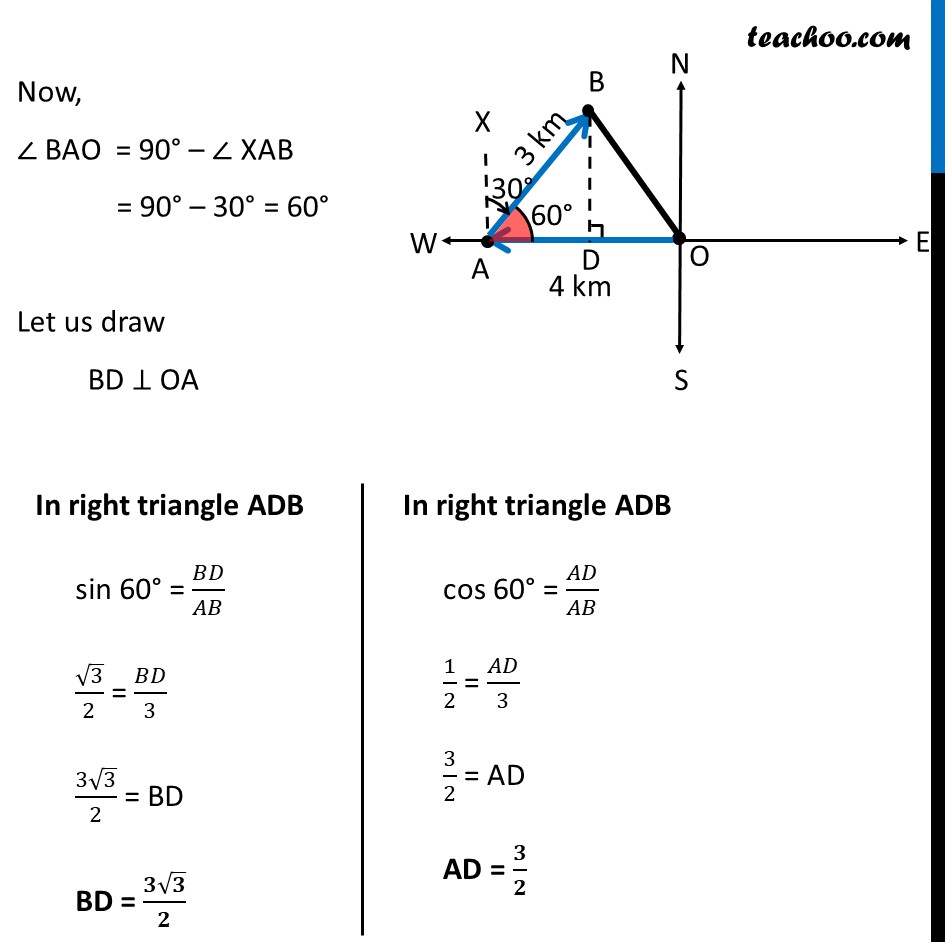
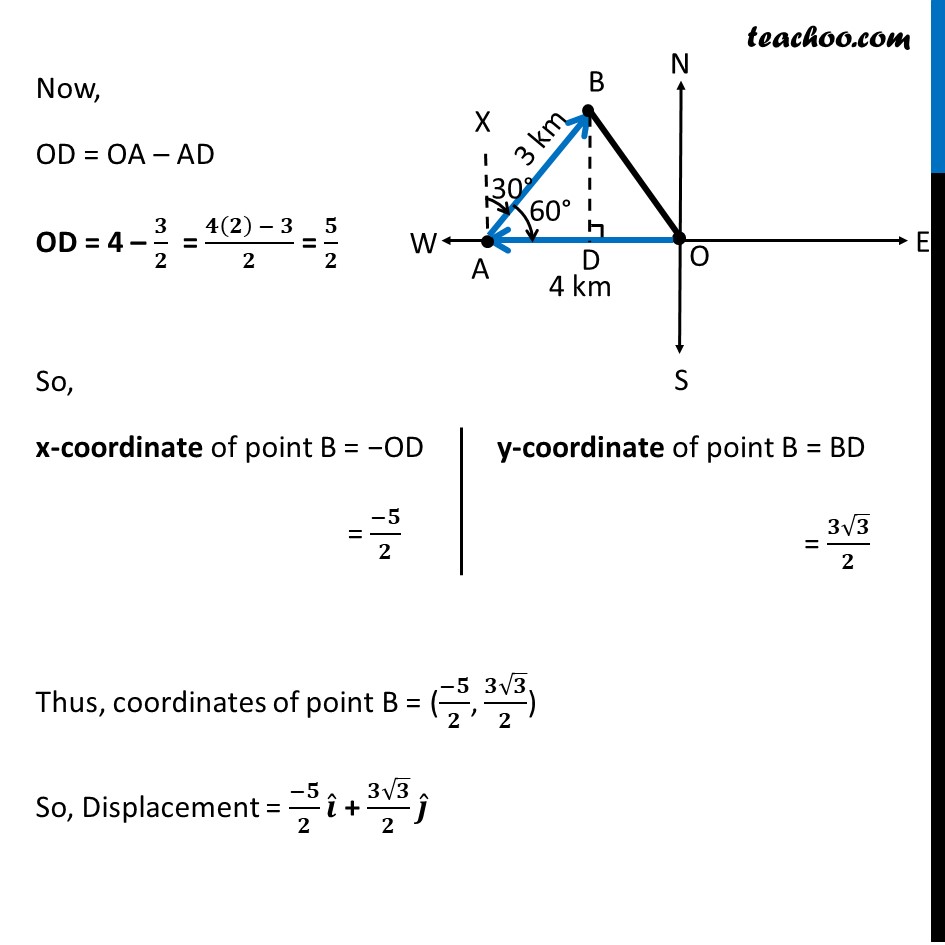
Misc 3 A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.Let initial point of departure be O(0, 0) & OA = 4km, AB = 3km ∠ XAB = 30° Here, Displacement will be vector (𝑂𝐵) ⃗ So, we need to find coordinates of B Rough Representation of 30° east of north Now, ∠ BAO = 90° – ∠ XAB = 90° – 30° = 60° Let us draw BD ⊥ OA In right triangle ADB sin 60° = 𝐵𝐷/𝐴𝐵 √3/2 = 𝐵𝐷/3 (3√3)/2 = BD BD = (𝟑√𝟑)/𝟐In right triangle ADB cos 60° = 𝐴𝐷/𝐴𝐵 1/2 = 𝐴𝐷/3 3/2 = AD AD = 𝟑/𝟐 Now, OD = OA – AD OD = 4 – 𝟑/𝟐 = (𝟒(𝟐) − 𝟑)/𝟐 = 𝟓/𝟐 So, x-coordinate of point B = −OD = (−𝟓)/𝟐 Thus, coordinates of point B = ((−𝟓)/𝟐, (𝟑√𝟑)/𝟐) So, Displacement = (−𝟓)/𝟐 𝒊 ̂ + (𝟑√𝟑)/𝟐 𝒋 ̂ y-coordinate of point B = BD = (𝟑√𝟑)/𝟐