Question 10 - Area between curve and curve - Chapter 8 Class 12 Application of Integrals
Last updated at April 16, 2024 by Teachoo
Area between curve and curve
Question 7
You are here
You are here
Chapter 8 Class 12 Application of Integrals
Concept wise
- Area under curve
- Area bounded by curve and horizontal or vertical line
- Area between curve and line
-
Area between curve and curve
Transcript
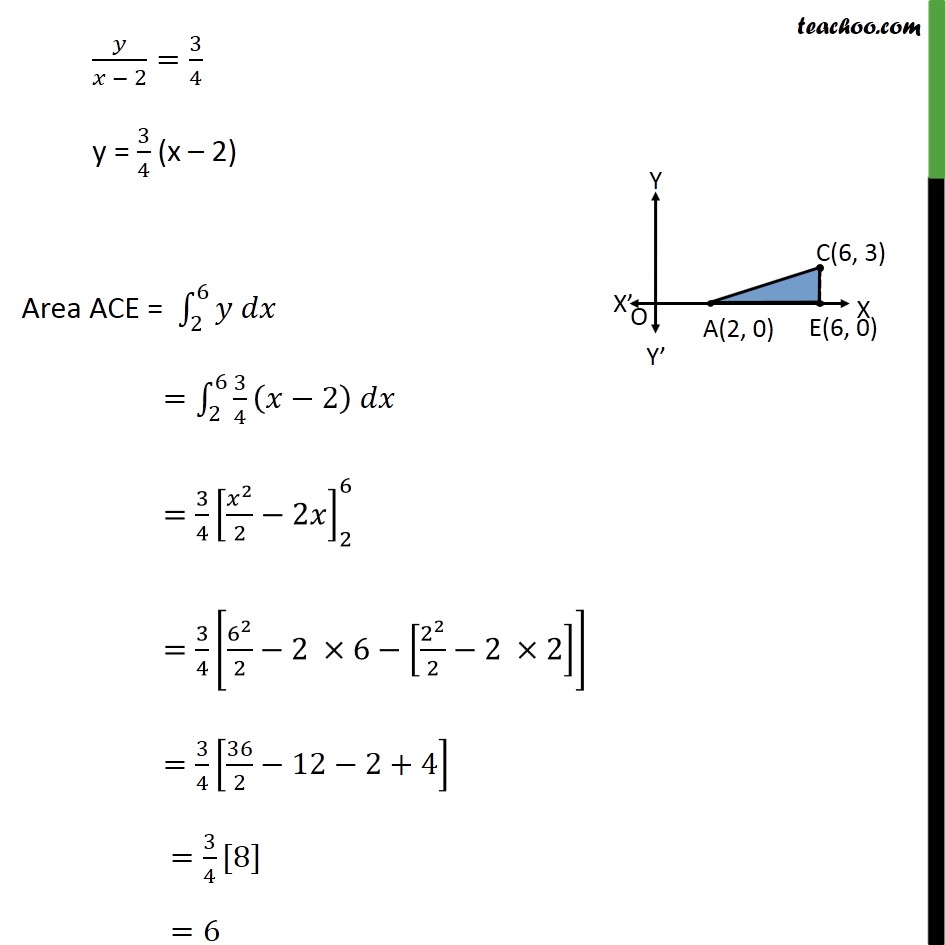
Question 10 Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5)& C (6, 3) Area of formed by points A(2, 0), B (4, 5)& C (6, 3) Step 1: Draw the figure Area ABD Area ABD= 2 4 equation of line AB Equation of line between A(2, 0) & B(4, 5) is 0 2 = 5 0 4 2 2 = 5 2 y = 5 2 (x 2) Area ABD = 2 4 = 2 4 5 2 (x 2) = 5 2 2 2 2 2 4 = 5 2 4 2 2 2 4 2 2 2 2 2 = 5 2 8 8 2+4 = 5 2 2 =5 Area BDEC Area BDEC = 4 6 equation of line BC Equation of line between B(4, 5) & C(6, 3) is 5 4 = 3 5 6 4 5 4 = 2 2 y 5 = 1(x 4) y 5 = x + 4 y = 9 x Area BDEC = 4 6 = 4 6 9 =9 4 6 4 6 =9 4 6 2 2 4 6 =9 6 4 1 2 6 2 4 2 =9 2 1 2 36 16 =18 10 = 8 Area ACE Area ACE= 2 6 equation of line AC Equation of line between A(2, 0) & C(6, 3) is 0 2 = 3 0 6 2 2 = 3 4 y = 3 4 (x 2) Area ACE = 2 6 = 2 6 3 4 2 = 3 4 2 2 2 2 6 = 3 4 6 2 2 2 6 2 2 2 2 2 = 3 4 36 2 12 2+4 = 3 4 [8] =6 Hence Area Required = Area ABD + Area BDEC Area ACE = 5 + 8 6 = 7 square units
