Question 9 - Miscellaneous - Chapter 8 Class 12 Application of Integrals

Transcript

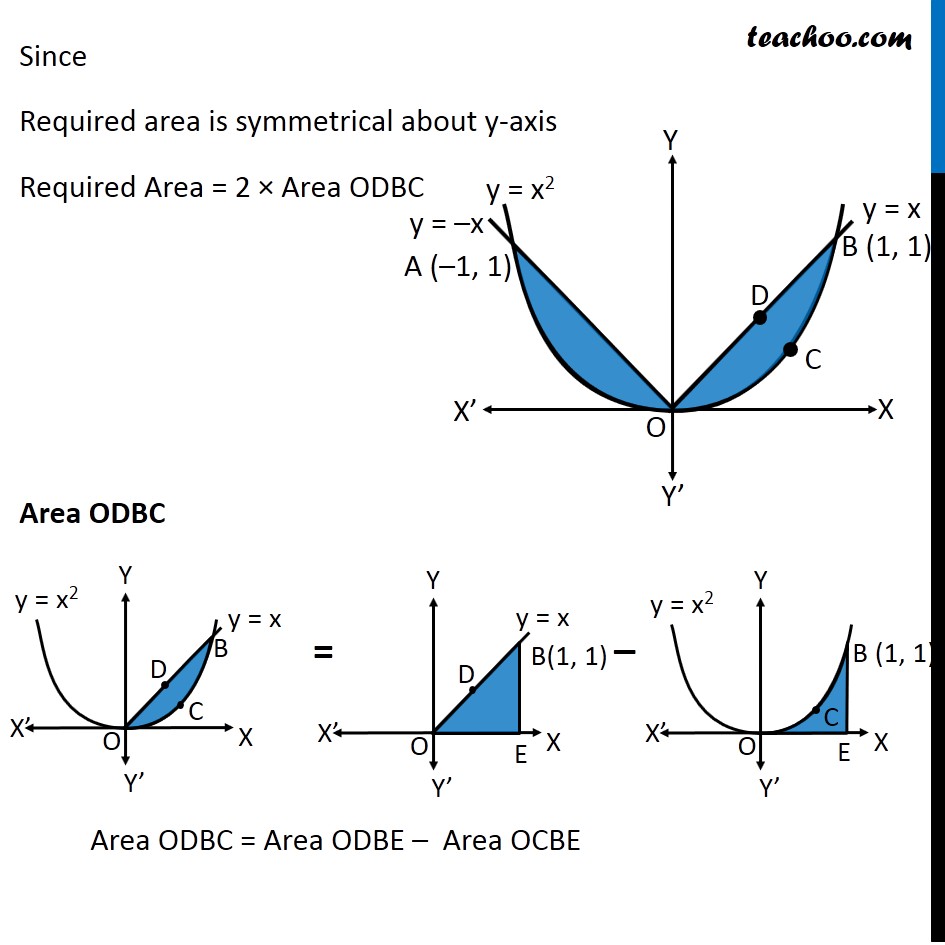
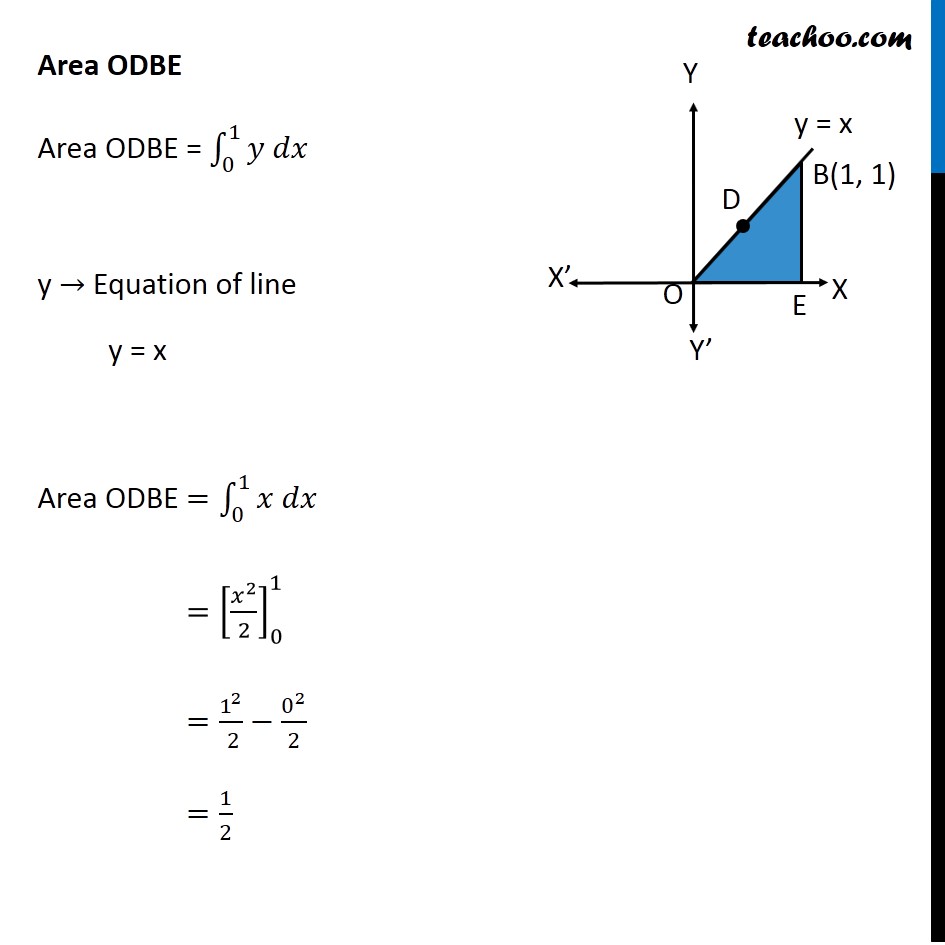
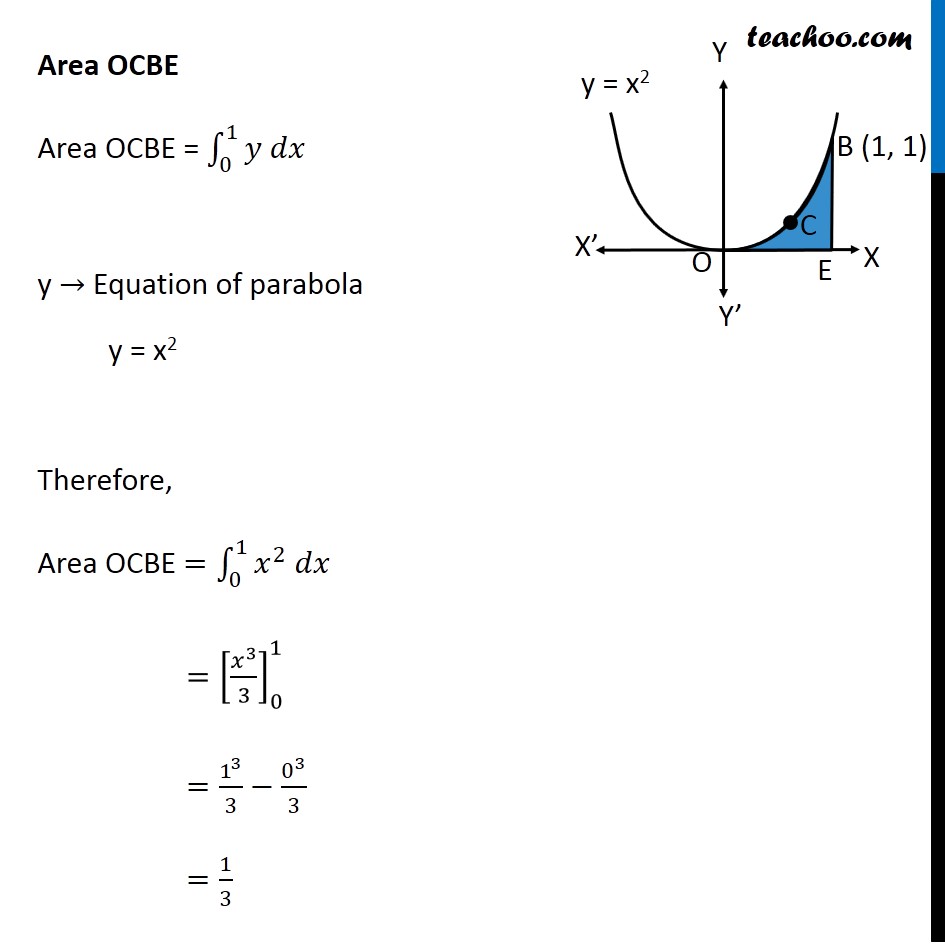
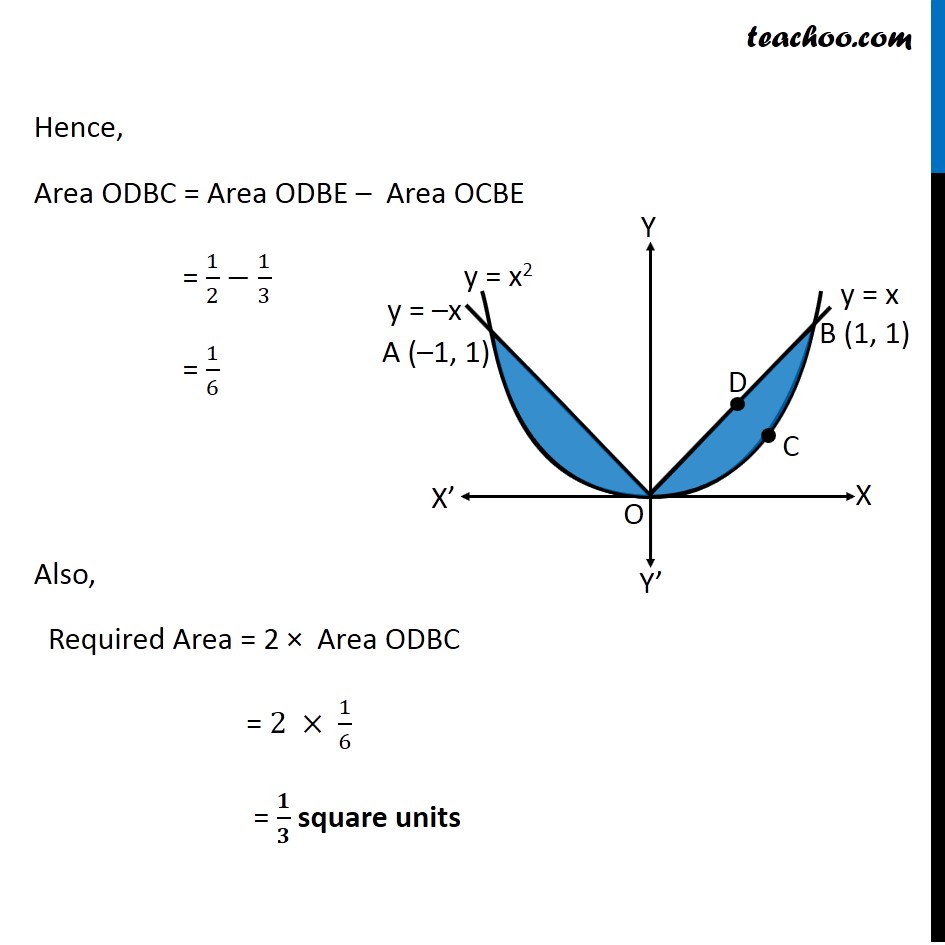
Question 9 Find the area bounded by curves {(𝑥, 𝑦) :𝑦≥ 𝑥2 and 𝑦=|𝑥|} Here, 𝑥^2=𝑦 is a parabola And y = |𝑥| ={█(𝑥, 𝑥≥0@&−𝑥, 𝑥<0)┤ So, we draw a parabola and two lines Point A is the intersection of parabola and line y = –x Point B is the intersection of parabola and line y = x Finding points A & B Point A Point A is intersection of y = x2 & y = –x Solving x2 = –x x2 + x = 0 x(x + 1) = 0 So, x = –1 & x = 0 For x = –1 y = –x = –(–1) = 1 So, point A (–1, 1) Point B Point B is intersection of y = x2 & y = x Solving x2 = x x2 – x = 0 x(x – 1) = 0 So, x = 1 & x = 0 For x = 1 y = x = 1 So, point B (1, 1) Since Required area is symmetrical about y-axis Required Area = 2 × Area ODBC Area ODBC Area ODBC = Area ODBE – Area OCBE Area ODBE Area ODBE = ∫_0^1▒〖𝑦 𝑑𝑥〗 y → Equation of line y = x Area ODBE =∫_0^1▒〖𝑥 𝑑𝑥〗 =[𝑥^2/2]_0^1 =1^2/( 2)−0^2/2 =1/2 Area OCBE Area OCBE = ∫_0^1▒〖𝑦 𝑑𝑥〗 y → Equation of parabola y = x2 Therefore, Area OCBE =∫_0^1▒〖𝑥^2 𝑑𝑥〗 =[𝑥^3/3]_0^1 =1^3/3−0^3/3 =1/3 Hence, Area ODBC = Area ODBE – Area OCBE = 1/2−1/3 = 1/6 Also, Required Area = 2 × Area ODBC = 2 × 1/6 = 𝟏/𝟑 square units