Question 8 - Miscellaneous - Chapter 8 Class 12 Application of Integrals

Transcript

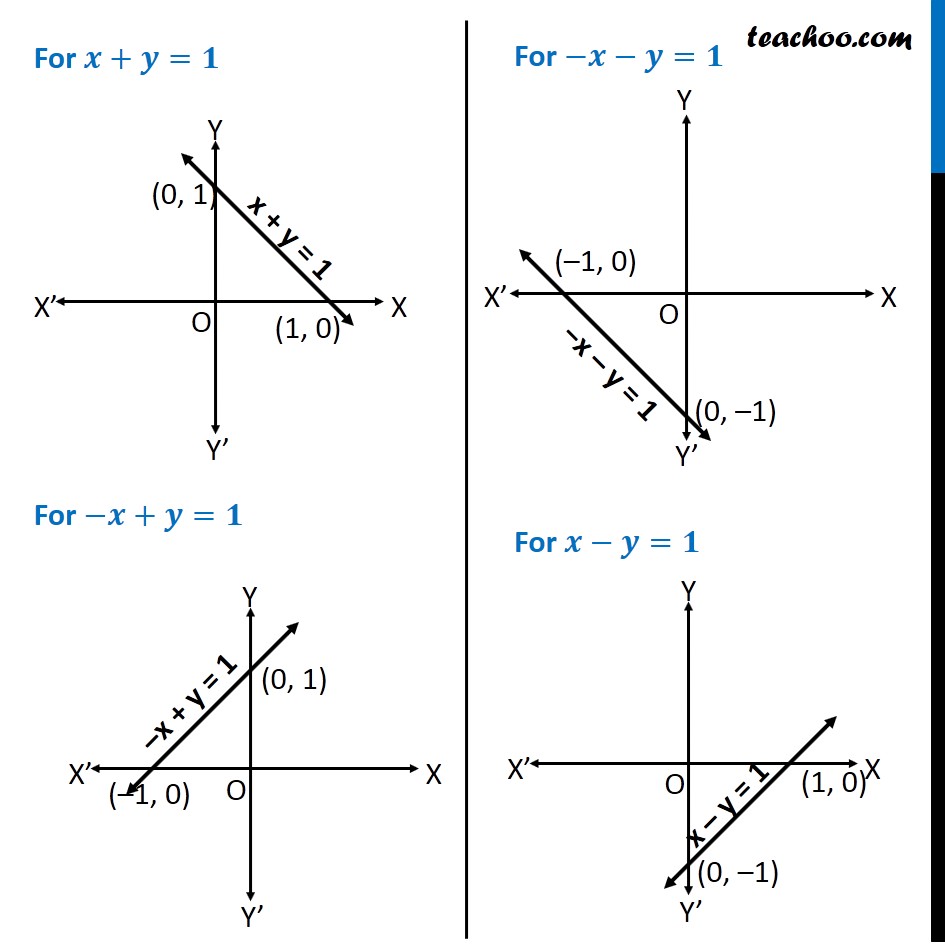
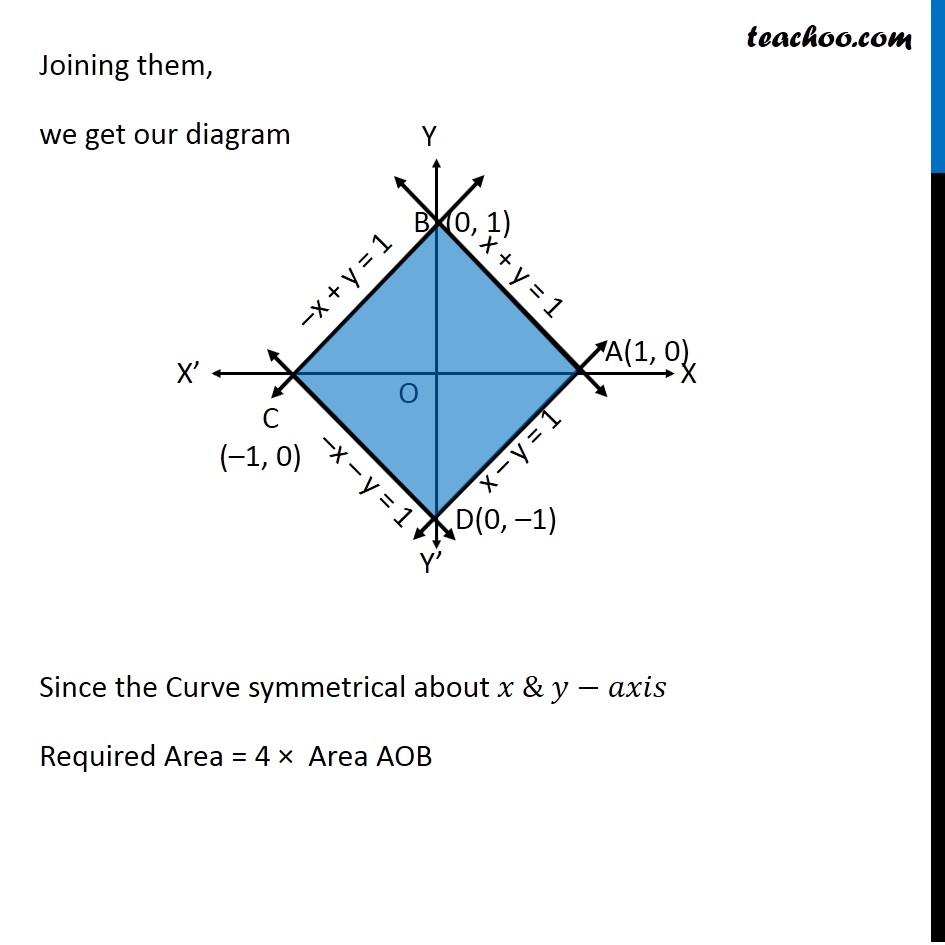
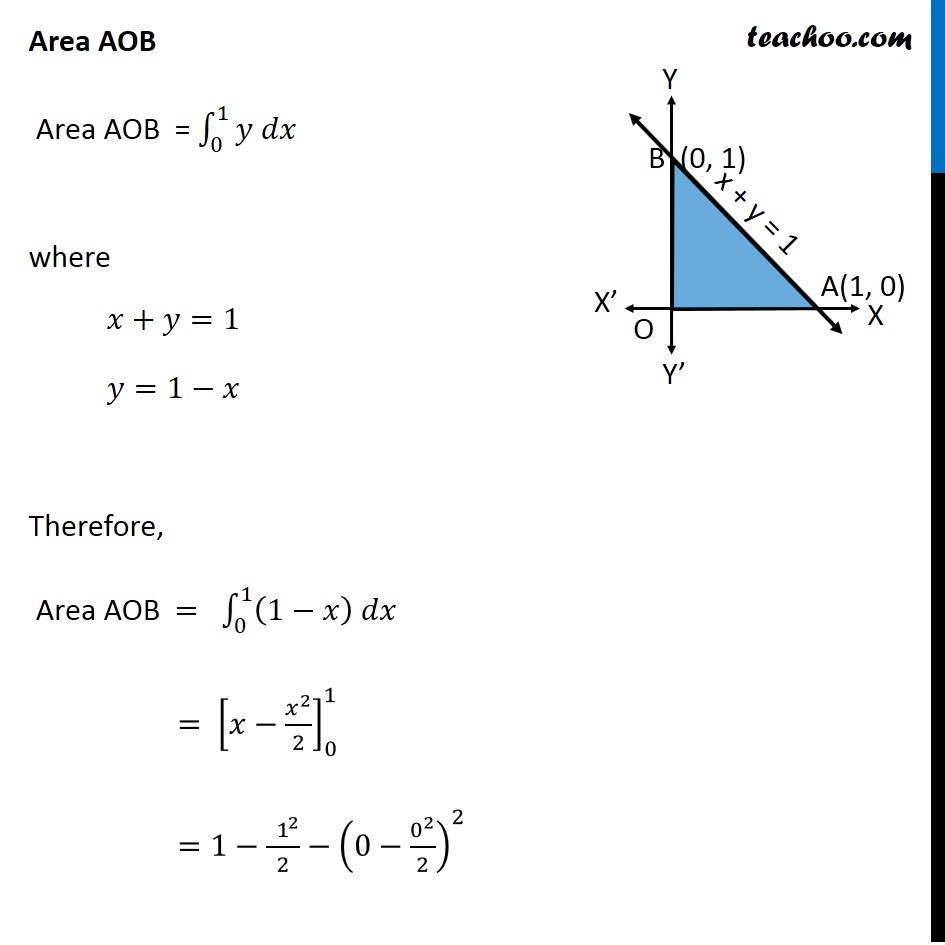
Question 8 Using the method of integration find the area bounded by the curve |𝑥|+|𝑦|=1 [Hint: The required region is bounded by lines 𝑥+𝑦= 1, 𝑥 –𝑦=1, –𝑥+𝑦 =1 and −𝑥 −𝑦=1 ] We know that "│" 𝑥"│"={█(𝑥, 𝑥≥0@&−𝑥, 𝑥<0)┤ & "│" 𝑦"│"={█(𝑦, 𝑦≥0@&−𝑦, 𝑦<0)┤ So, we can write │𝑥"│+│" 𝑦"│"=1 as {█(█(█( 𝑥+𝑦=1 𝑓𝑜𝑟 𝑥>0 , 𝑦>0@−𝑥+𝑦=1 𝑓𝑜𝑟 𝑥<0 𝑦>0)@█( 𝑥−𝑦 =1 𝑓𝑜𝑟 𝑥>0 , 𝑦<0@−𝑥−𝑦=1 𝑓𝑜𝑟 𝑥<0 𝑦<0)))┤ For 𝒙+𝒚=𝟏 For −𝒙+𝒚=𝟏 For −𝒙−𝒚=𝟏 For 𝒙−𝒚=𝟏 Joining them, we get our diagram Since the Curve symmetrical about 𝑥 & 𝑦−𝑎𝑥𝑖𝑠 Required Area = 4 × Area AOB Area AOB Area AOB = ∫_0^1▒〖𝑦 𝑑𝑥〗 where 𝑥+𝑦=1 𝑦=1−𝑥 Therefore, Area AOB = ∫_0^1▒〖(1−𝑥) 𝑑𝑥〗 = [𝑥−𝑥^2/2]_0^1 =1−〖 1〗^2/2−(0−0^2/2)^2 =1−1/2 =1/2 Hence, Required Area = 4 × Area AOB = 4 × 1/2 = 2 square units