Question 4 - Area between curve and line - Chapter 8 Class 12 Application of Integrals
Last updated at Dec. 16, 2024 by Teachoo
Area between curve and line
Question 2
You are here
You are here
You are here
You are here
Chapter 8 Class 12 Application of Integrals
Concept wise
- Area under curve
- Area bounded by curve and horizontal or vertical line
-
Area between curve and line
- Area between curve and curve
Transcript
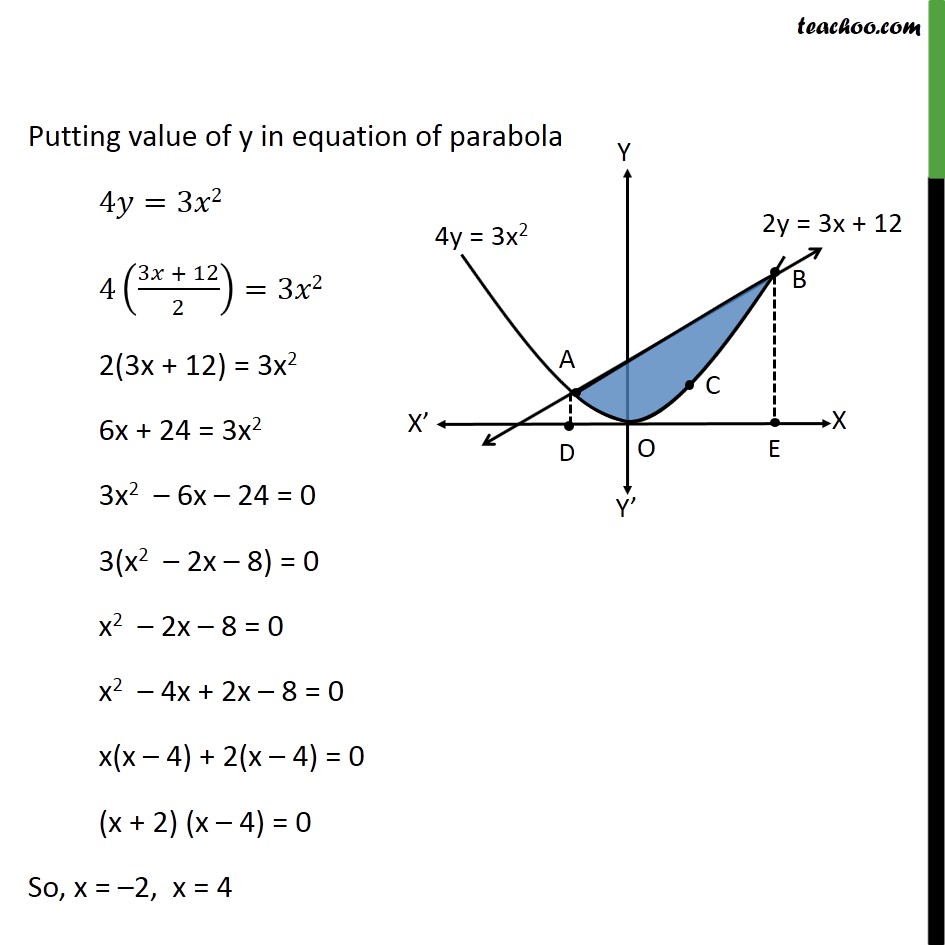
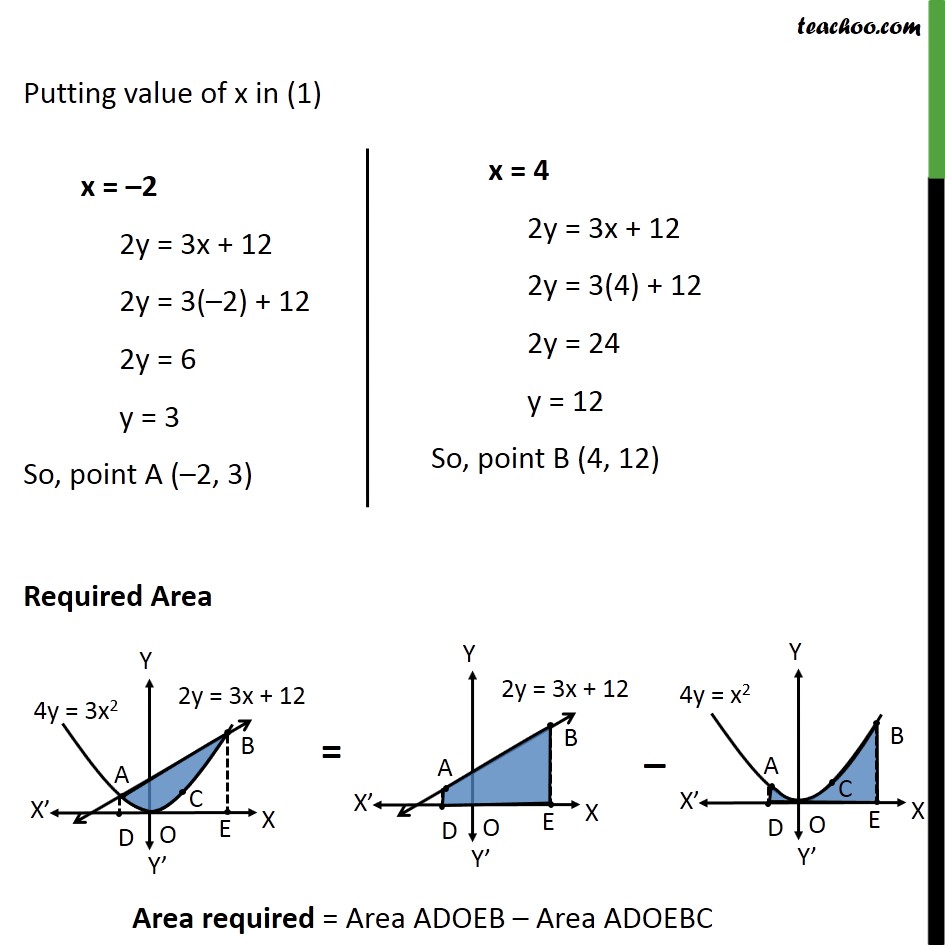
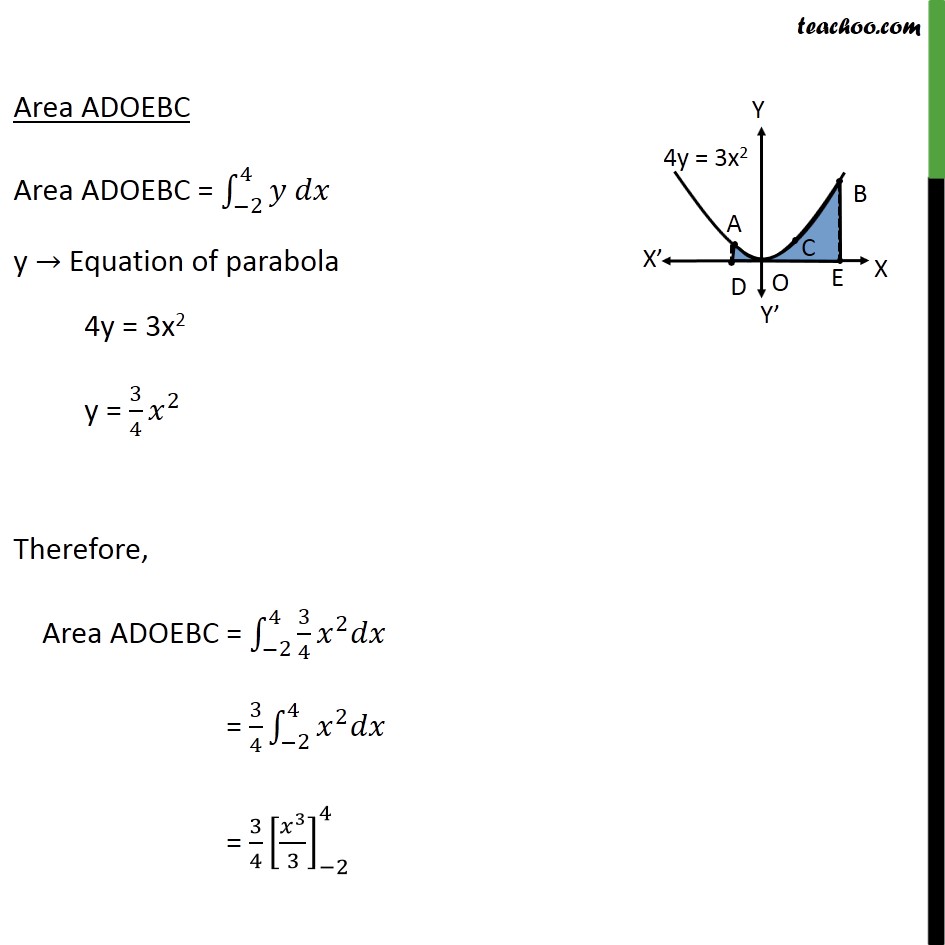
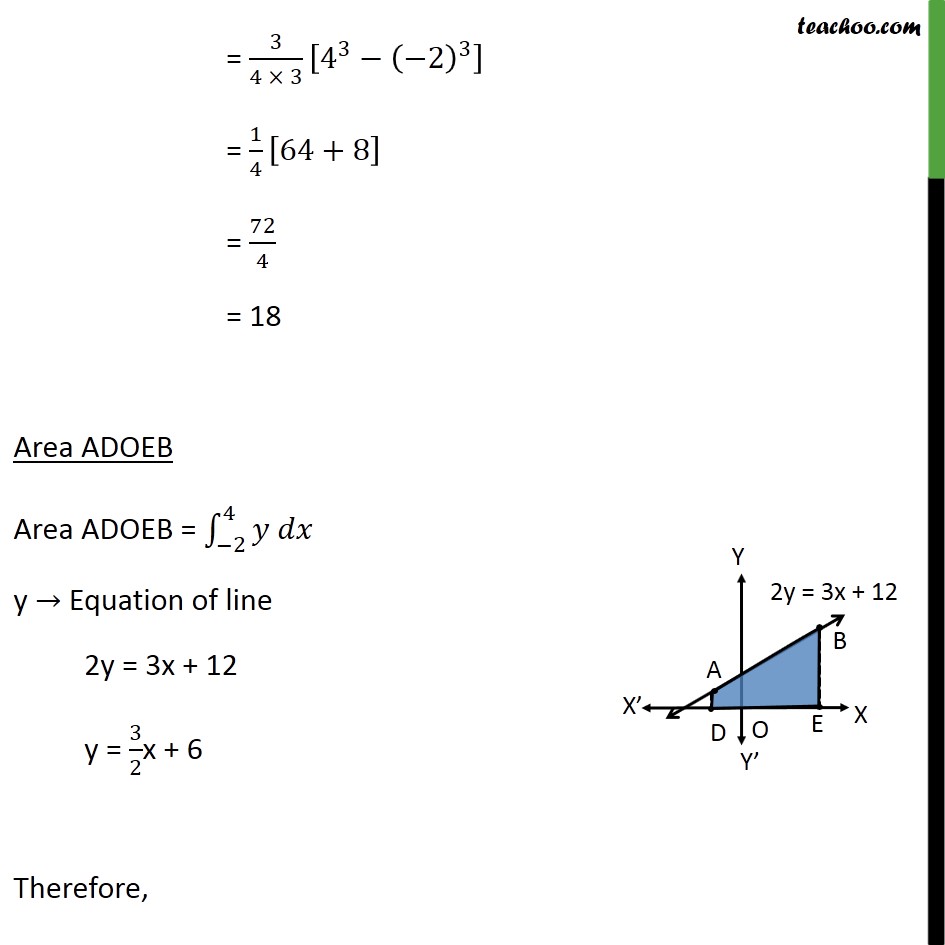
Question 4 Find the area enclosed by the parabola 4𝑦=3𝑥2 and the line 2𝑦 = 3𝑥 + 12 Area ADOEB = ∫1_(−2)^4▒〖(3/2 𝑥+6) 𝑑𝑥〗 = [3/2 (𝑥^2/2)+6𝑥]_(−2)^4 = [(3𝑥^2)/4+6𝑥]_(−2)^4 = [(3(4^2))/4+6(4)] – [(3〖(−2)〗^2)/4+6(−2)] = [12+24] – [3−12] = 36 + 9 = 45 Area required = Area ADOEB – Area ADOEBC = 45 – 18 = 27
