Misc 3 - Chapter 8 Class 12 Application of Integrals

Last updated at Aug. 11, 2023 by Teachoo

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

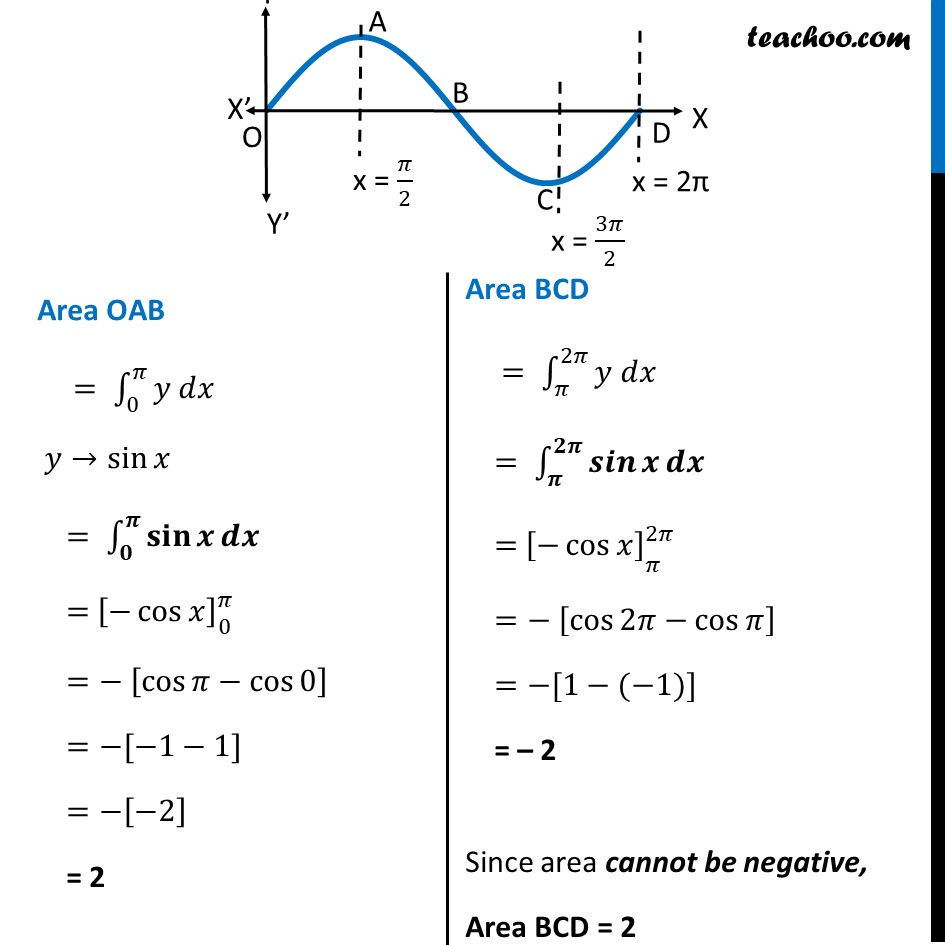
Misc 3 Find the area bounded by the curve 𝑦=sin⁡𝑥 between 𝑥=0 and 𝑥=2𝜋 Area Required = Area OAB + Area BCD Area OAB = ∫_0^𝜋▒〖𝑦 𝑑𝑥〗 𝑦→sin⁡𝑥 = ∫_𝟎^𝝅▒〖𝐬𝐢𝐧⁡𝒙 𝒅𝒙〗 = [−cos⁡𝑥 ]_█( @0)^𝜋 =− [cos⁡𝜋−cos⁡0 ] =−[−1−1] =−[−2] = 2 Area BCD = ∫_𝜋^2𝜋▒〖𝑦 𝑑𝑥〗 = ∫_𝝅^𝟐𝝅▒〖𝒔𝒊𝒏⁡𝒙 𝒅𝒙〗 = [−cos⁡𝑥 ]_█( @ @𝜋)^2𝜋 =− [cos⁡2𝜋−cos⁡𝜋 ] =−[1−(−1)] = – 2 Since area cannot be negative, Area BCD = 2 Hence, Area Required = Area OAB + Area BCD = 2+2 = 𝟒 square units

Next: Misc 4 (MCQ) → Ask a doubt

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular