Question 11 - Examples - Chapter 8 Class 12 Application of Integrals

Transcript

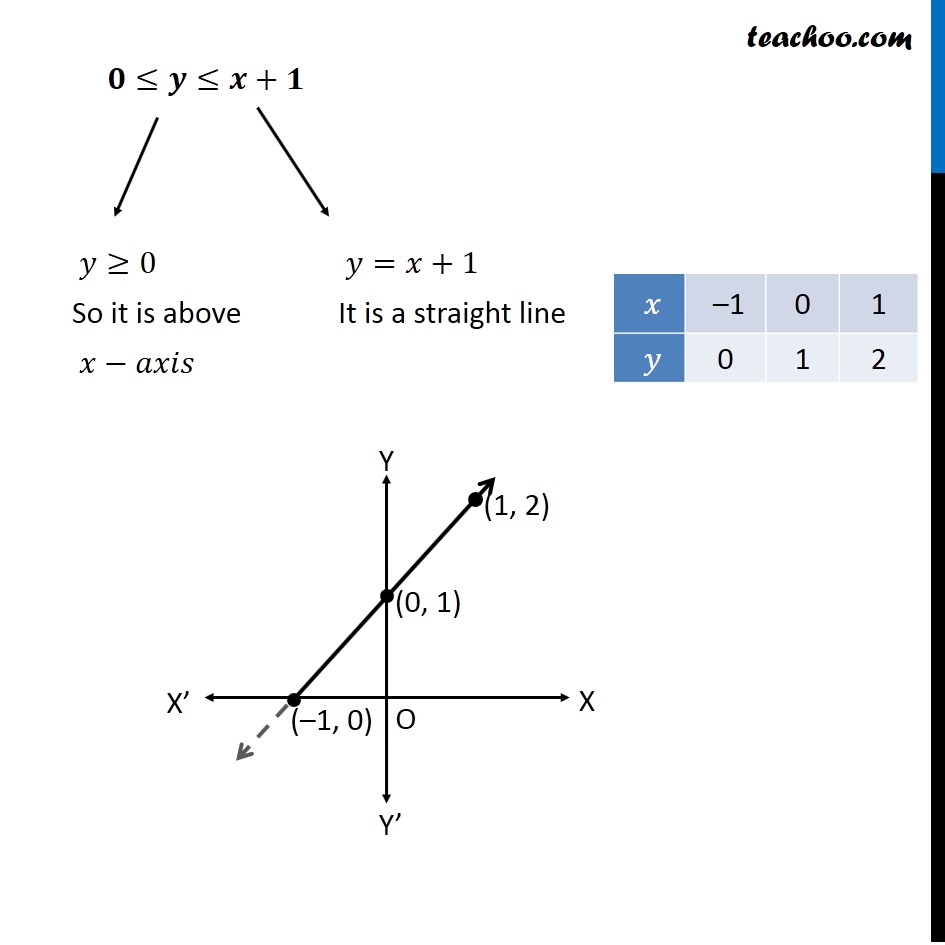
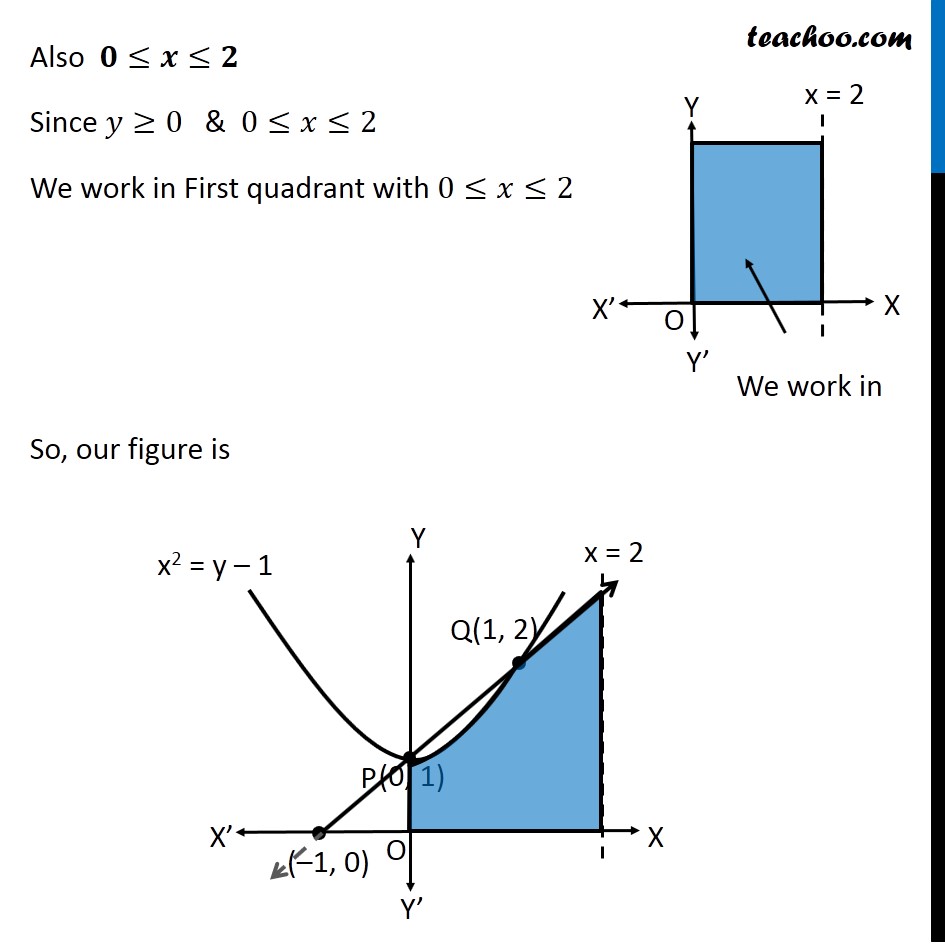
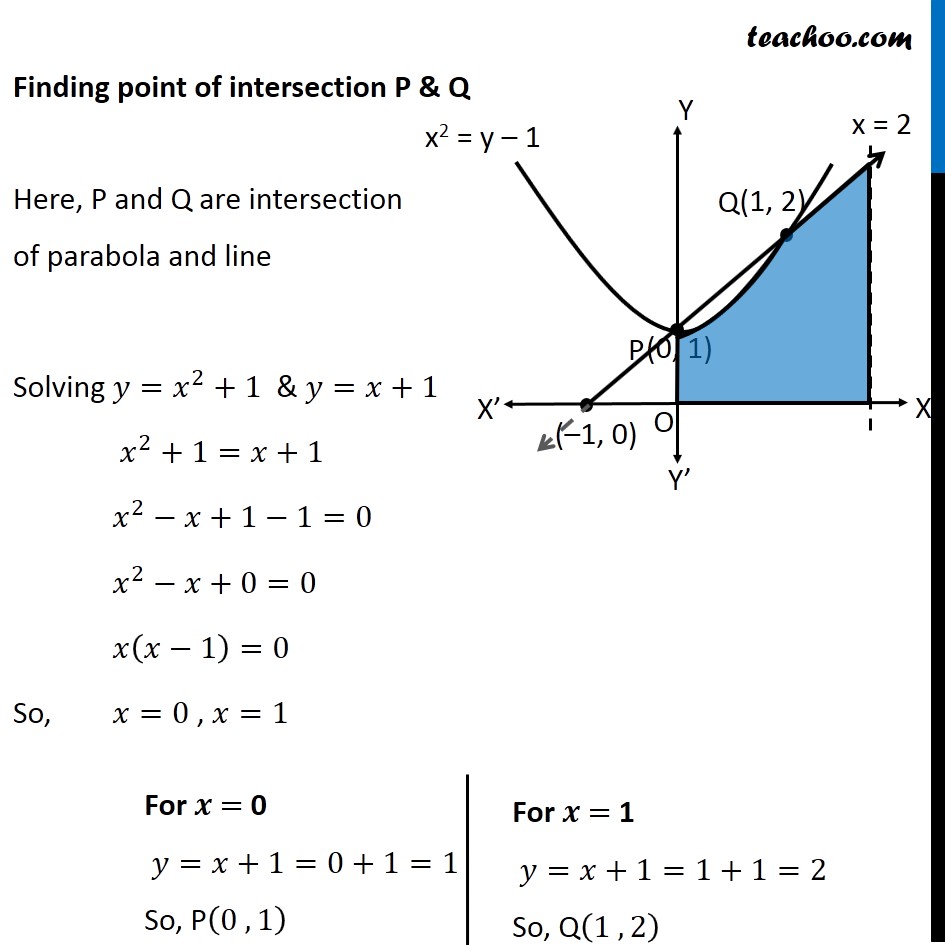
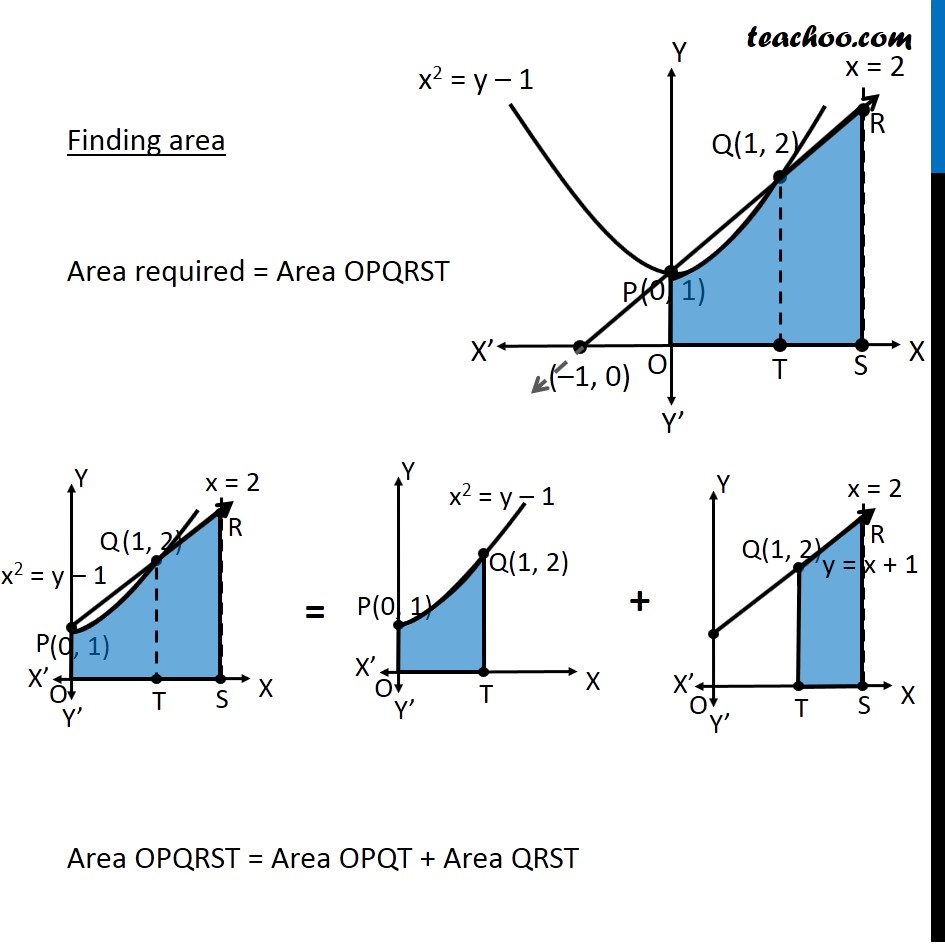
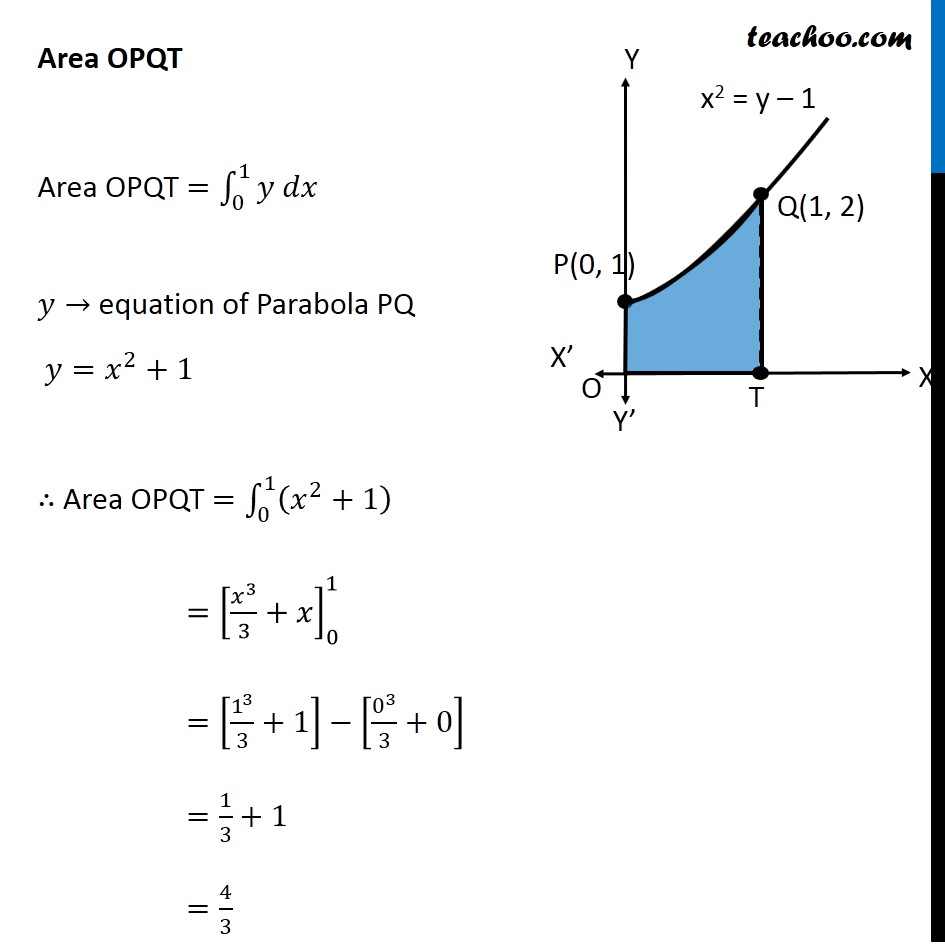
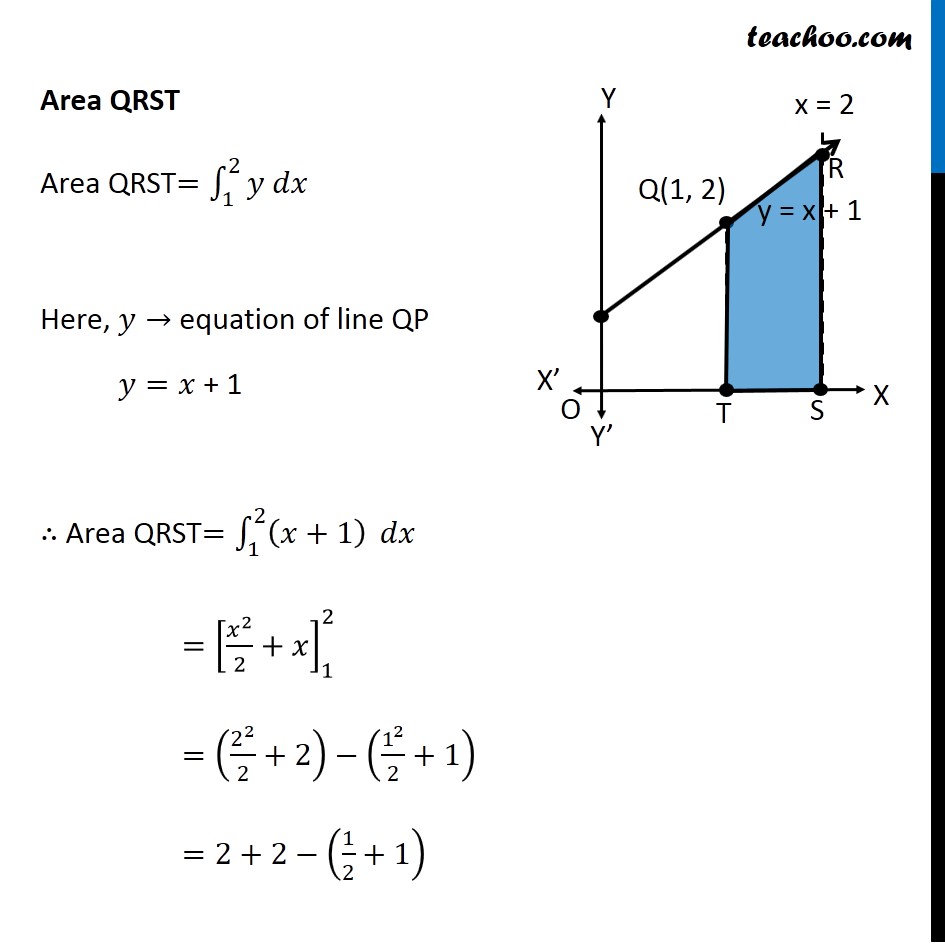
Question 11 Find the area of the region {(𝑥, 𝑦) : 0 ≤ 𝑦 ≤ 𝑥2 + 1, 0 ≤ 𝑦 ≤ 𝑥 + 1, 0 ≤ 𝑥 ≤ 2} Here, 𝟎≤𝒚≤𝒙^𝟐+𝟏 𝑦≥0 So it is above 𝑥−𝑎𝑥𝑖𝑠 𝑦=𝑥^2+1 i.e. 𝑥^2=𝑦−1 So, it is a parabola 𝟎≤𝒚≤𝒙+𝟏 𝑦≥0 So it is above 𝑥−𝑎𝑥𝑖𝑠 𝑦=𝑥+1 It is a straight line Also 𝟎≤𝒙≤𝟐 Since 𝑦≥0 & 0≤𝑥≤2 We work in First quadrant with 0≤𝑥≤2 So, our figure is Finding point of intersection P & Q Here, P and Q are intersection of parabola and line Solving 𝑦=𝑥^2+1 & 𝑦=𝑥+1 𝑥^2+1=𝑥+1 𝑥^2−𝑥+1−1=0 𝑥^2−𝑥+0=0 𝑥(𝑥−1)=0 So, 𝑥=0 , 𝑥=1 For 𝒙 = 0 𝑦=𝑥+1=0+1=1 So, P(0 , 1) For 𝒙 = 1 𝑦=𝑥+1=1+1=2 So, Q(1 , 2) Finding area Area required = Area OPQRST Area OPQRST = Area OPQT + Area QRST Area OPQT Area OPQT =∫_0^1▒〖𝑦 𝑑𝑥〗 𝑦→ equation of Parabola PQ 𝑦=𝑥^2+1 ∴ Area OPQT =∫_0^1▒(𝑥^2+1) =[𝑥^3/3+𝑥]_0^1 =[1^3/3+1]−[0^3/3+0] =1/3+1 =4/3 Area QRST Area QRST=∫_1^2▒〖𝑦 𝑑𝑥〗 Here, 𝑦→ equation of line QP 𝑦=𝑥 + 1 ∴ Area QRST=∫_1^2▒(𝑥+1) 𝑑𝑥 =[𝑥^2/2+𝑥]_1^2 =(2^2/2+2)−(1^2/2+1) =2+2−(1/2+1) =4−3/2 =5/2 Thus, Area Required = Area OPQT + Area QPST = 4/3+5/2 = (8 + 15)/6 = 𝟐𝟑/𝟔 square units