

Area bounded by curve and horizontal or vertical line
Area bounded by curve and horizontal or vertical line
Last updated at December 16, 2024 by Teachoo



Transcript
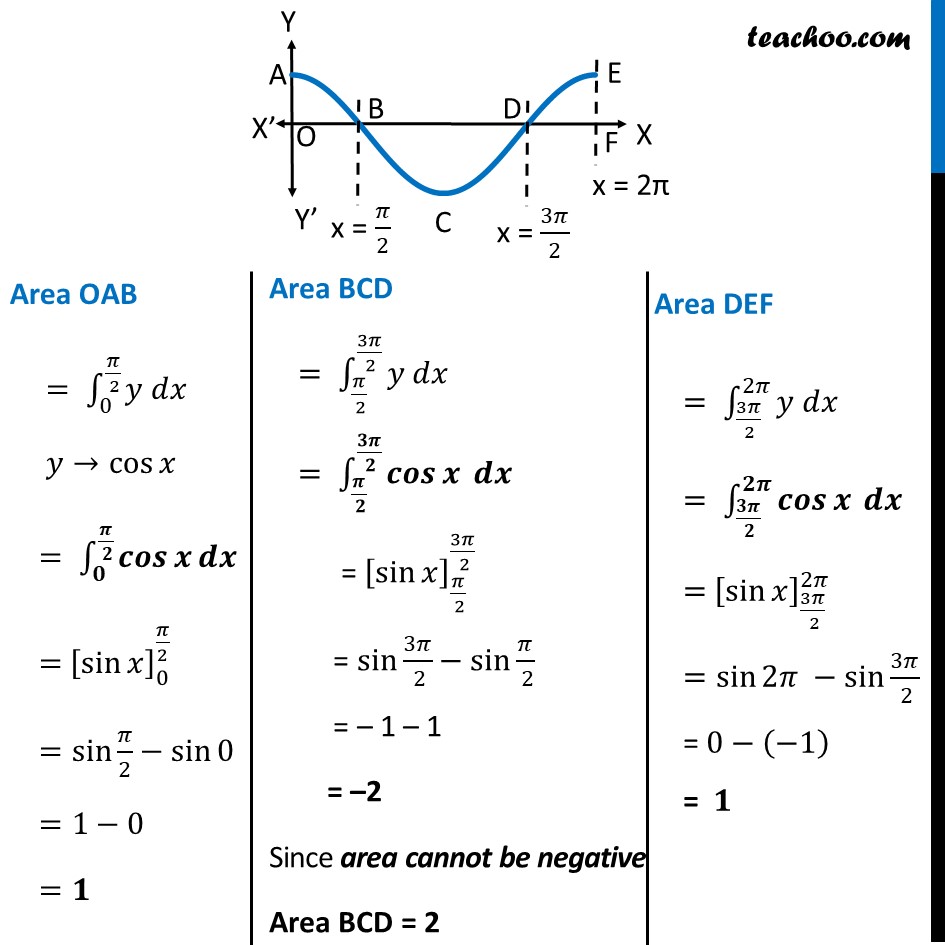
Example 4 Find the area bounded by the curve 𝑦=cos𝑥 between 𝑥=0 and 𝑥=2𝜋Area OAB = ∫_0^(𝜋/( 2))▒〖𝑦 𝑑𝑥〗 𝑦→cos𝑥 = ∫_𝟎^(𝝅/( 𝟐))▒〖𝒄𝒐𝒔𝒙 𝒅𝒙〗 = [sin𝑥 ]_0^(𝜋/2) =sin〖𝜋/2−sin0 〗 =1−0 =𝟏 Area BCD = ∫_(𝜋/( 2))^(3𝜋/( 2))▒〖𝑦 𝑑𝑥〗 = ∫_(𝝅/( 𝟐))^(𝟑𝝅/( 𝟐))▒〖𝒄𝒐𝒔𝒙 𝒅𝒙〗 = [sin𝑥 ]_(𝜋/( 2))^(3𝜋/( 2)) = sin 3𝜋/( 2)−sin〖𝜋/( 2)〗 = – 1 – 1 = –2 Since area cannot be negative Area BCD = 2 Area DEF = ∫_(3𝜋/( 2))^2𝜋▒〖𝑦 𝑑𝑥〗 = ∫_(𝟑𝝅/( 𝟐))^𝟐𝝅▒〖𝒄𝒐𝒔𝒙 𝒅𝒙〗 = [sin𝑥 ]_(3𝜋/( 2))^2𝜋 =sin2𝜋 −sin〖3𝜋/( 2)〗 = 0−(−1) = 𝟏 Therefore Area Required = Area OAB + Area BCD + Area DEF = 1 + 2 + 1 = 4 square unit