Question 8 - Area between curve and curve - Chapter 8 Class 12 Application of Integrals

Transcript

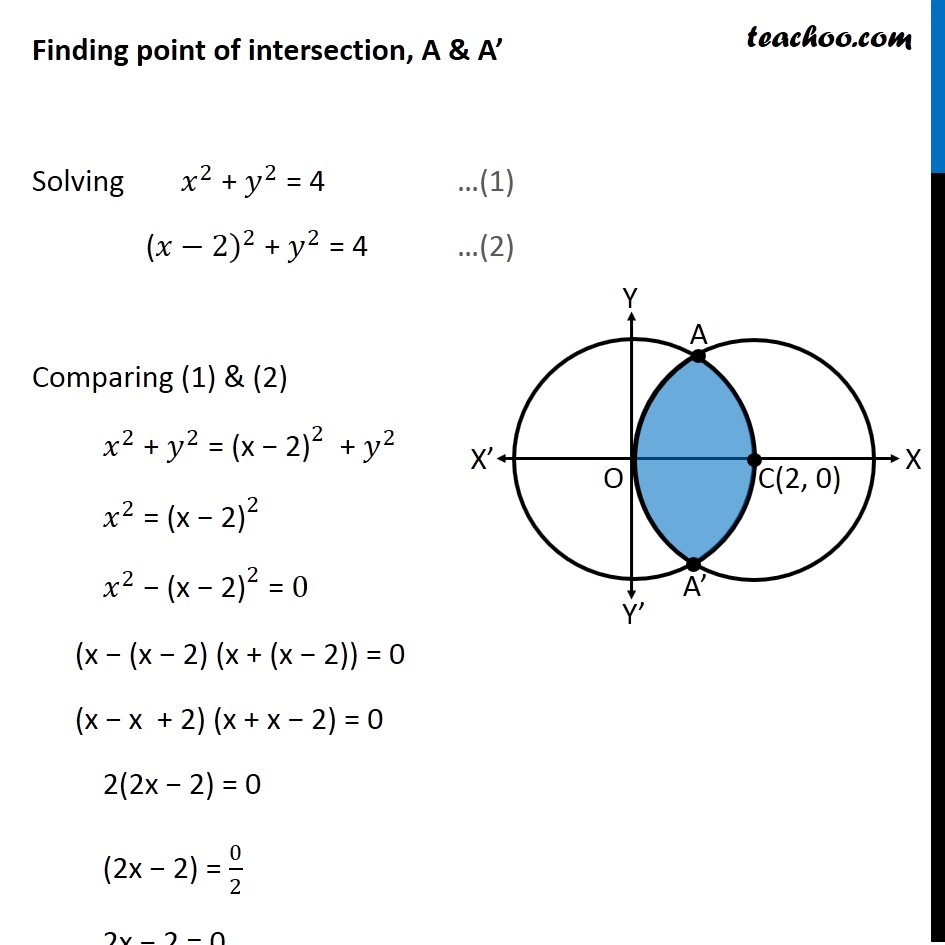
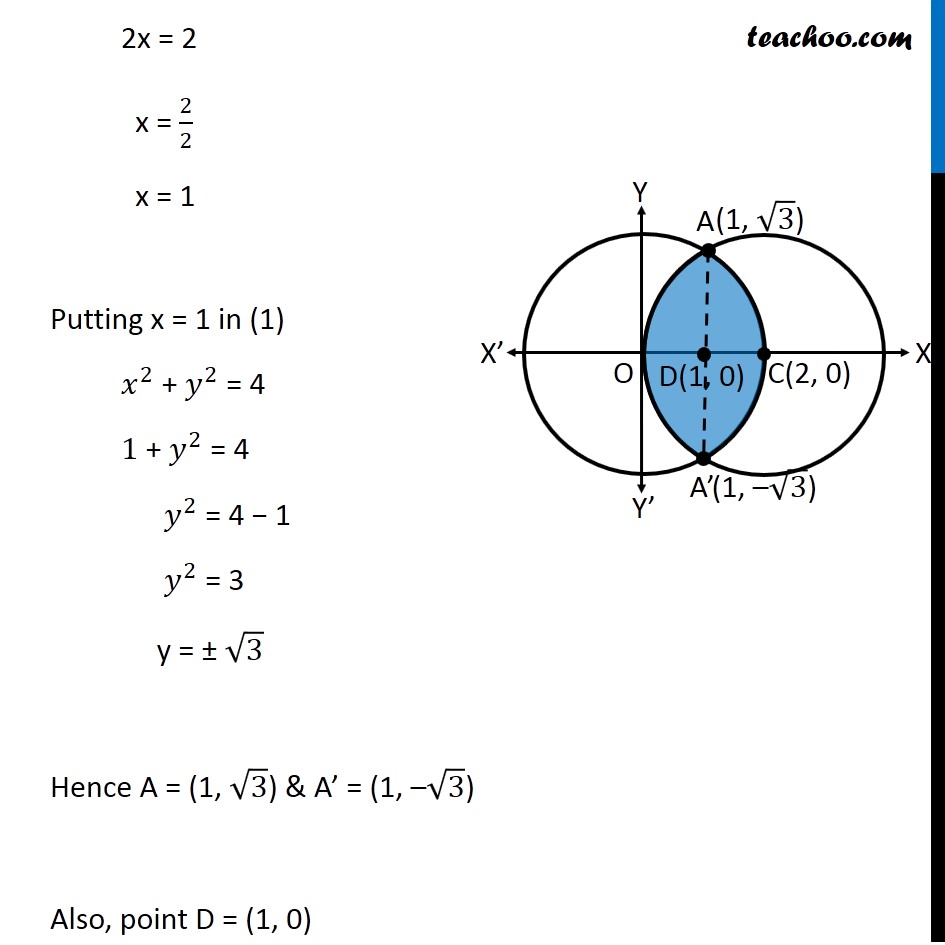
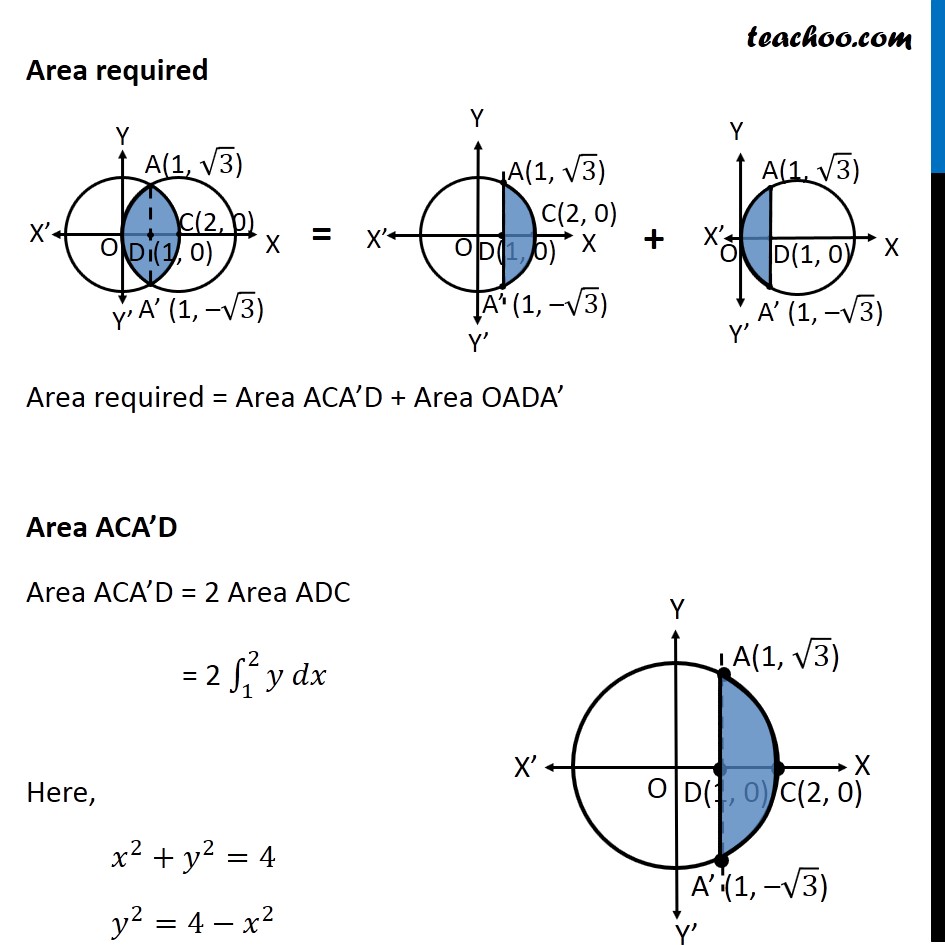
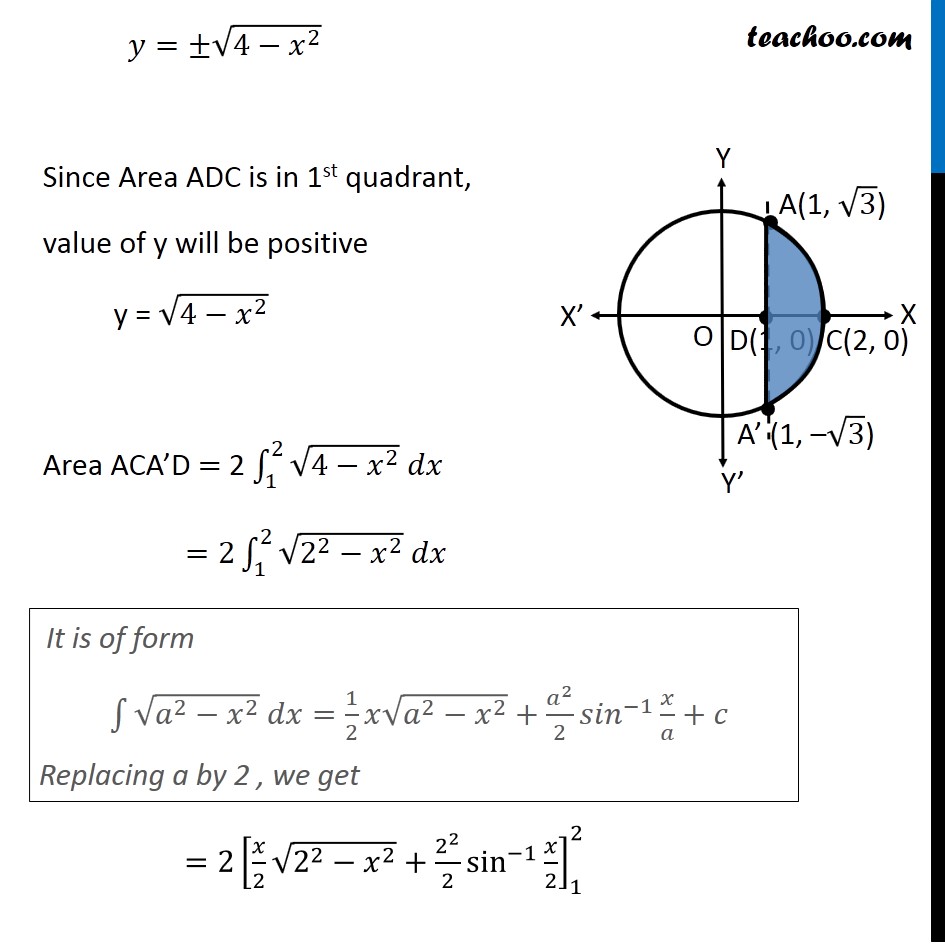
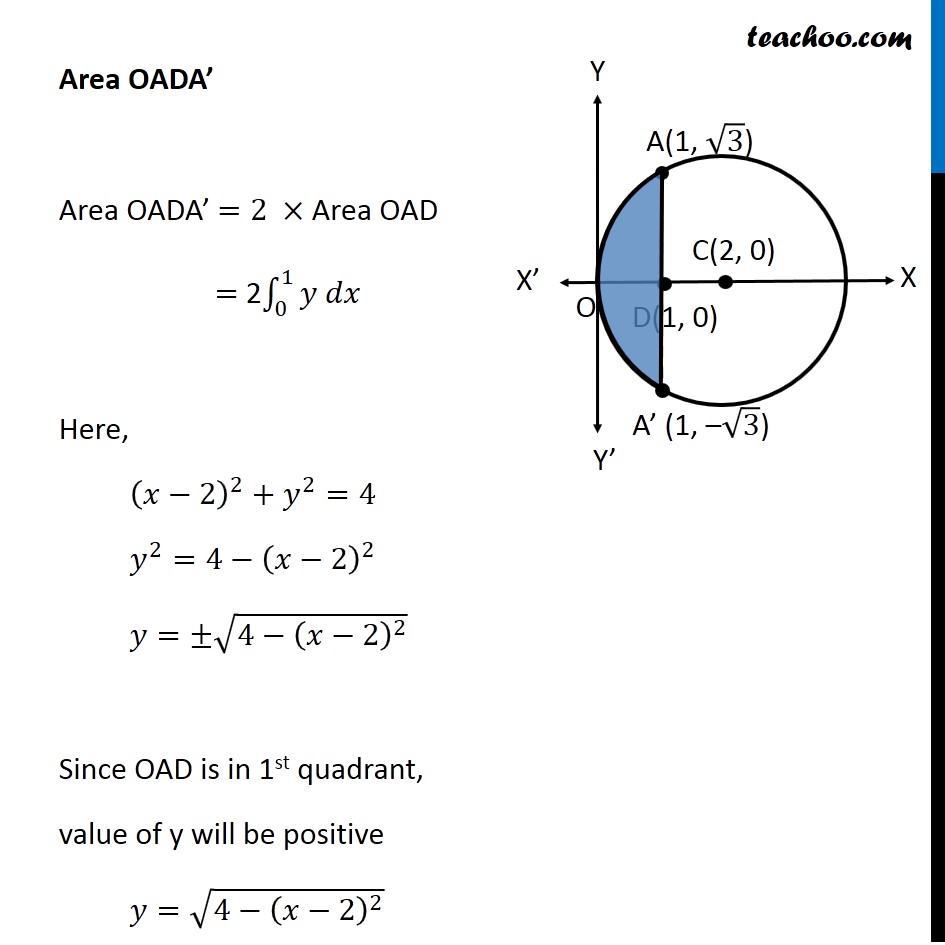
Question 8 Find the area of the region enclosed between the two circles: 𝑥2+𝑦2=4 and (𝑥 –2)2+𝑦2=4 First we find center and radius of both circles 𝑥^2+ 𝑦^2 = 4 〖(𝑥−0)〗^2 + 〖(𝑦−0)〗^2 = 2^2 Thus, Center = (0, 0) Radius = 2 (𝑥−2)^2 + 𝑦^2 = 4 〖(𝑥−2)〗^2 + 〖(𝑦−0)〗^2 = 2^2 Thus, Center = (2, 0) Radius = 2 Drawing figure Finding point of intersection, A & A’ Solving 𝑥^2 + 𝑦^2 = 4 …(1) (〖𝑥−2)〗^2 + 𝑦^2 = 4 …(2) Comparing (1) & (2) 𝑥^2 + 𝑦^2 = 〖"(x − 2)" 〗^2 + 𝑦^2 𝑥^2 = 〖"(x − 2)" 〗^2 𝑥^2 − 〖"(x − 2)" 〗^2 = 0 (x − (x − 2) (x + (x − 2)) = 0 (x − x + 2) (x + x − 2) = 0 2(2x − 2) = 0 (2x − 2) = 0/2 2x − 2 = 0 2x = 2 x = 2/2 x = 1 Putting x = 1 in (1) 𝑥^2 + 𝑦^2 = 4 1 + 𝑦^2 = 4 𝑦^2 = 4 − 1 𝑦^2 = 3 y = ± √3 Hence A = (1, √3) & A’ = (1, –√3) Also, point D = (1, 0) Area required Area required = Area ACA’D + Area OADA’ Area ACA’D Area ACA’D = 2 Area ADC = 2 ∫_1^2▒〖𝑦 𝑑𝑥〗 Here, 𝑥^2+𝑦^2=4 𝑦^2=4−𝑥^2 𝑦=±√(4−𝑥^2 ) Since Area ADC is in 1st quadrant, value of y will be positive y = √(4−𝑥^2 ) Area ACA’D = 2 ∫_1^2▒〖√(4−𝑥^2 ) 𝑑𝑥〗 =2∫_1^2▒〖√(2^2−𝑥^2 ) 𝑑𝑥〗 =2[𝑥/2 √(2^2−𝑥^2 )+2^2/2 sin^(−1)⁡〖𝑥/2〗 ]_1^2 It is of form ∫1▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥=1/2 𝑥√(𝑎^2−𝑥^2 )〗+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖𝑥/𝑎+𝑐〗 Replacing a by 2 , we get =〖2[𝑥/2 √(4−𝑥^2 )+2 sin^(−1)⁡〖𝑥/2〗 ]〗_1^2 =2[2/2 √(4−2^2 )+2 sin^(−1)⁡〖2/2−[1/2 √(4−1^2 )+2 sin^(−1)⁡〖1/2〗 ]〗 ] =2[1.√(4−4)+2 sin^(−1)⁡〖1−[1/2 √(4−1)+2 sin^(−1)⁡〖1/2〗 ]〗 ] =2[1.0+2𝜋/2⁡〖1−[1/2 √3+2𝜋/6]〗 ] =2[𝜋−√3/2−𝜋/3] =2[2𝜋/3−√3/2] =𝟒𝝅/𝟑−√𝟑 Area OADA’ Area OADA’ =2 × Area OAD = 2∫_0^1▒〖𝑦 𝑑𝑥〗 Here, (𝑥−2)^2+𝑦^2=4 𝑦^2=4−(𝑥−2)^2 𝑦=±√(4−(𝑥−2)^2 ) Since OAD is in 1st quadrant, value of y will be positive 𝑦=√(4−(𝑥−2)^2 ) Hence, Area OADA’ = 2∫_0^1▒〖√(4−(𝑥−2)^2 ) 𝑑𝑥〗 Putting t = (𝑥−2) Diff. w.r.t. 𝑥 𝑑𝑡/𝑑𝑥=1 𝑑𝑡 =𝑑𝑥 So, Area OADA’ = 2∫_0^1▒〖√(4−(𝑥−2)^2 ) 𝑑𝑥〗 =2∫_(−2)^(−1)▒〖√(4−𝑡^2 ) 𝑑𝑡〗 =2∫_(−2)^(−1)▒〖√(2^2−𝑡^2 ) 𝑑𝑡〗 It is of form ∫1▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥=1/2 𝑥√(𝑎^2−𝑥^2 )〗+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖𝑥/𝑎+𝑐〗 Replacing a with 2 & x with t, we get =2[𝑡/2 √(2^2−𝑡^2 )+2^2/2 sin^(−1)⁡〖𝑡/2〗 ]_(−2)^(−1) = 2[(−1)/( 2) √(2^2−(−1)^2 )+2 sin^(−1) (−1)/2]−2[(−2)/( 2) √(2^2−(−2)^2 )+2 sin^(−1) (−2)/2] = 2[(−1)/( 2) √(4−1)+2sin^(−1) ((−1)/2)]−2[−1√(4−4)+2sin^(−1) (−1)] = 2[(−1)/( 2)×√3+2 sin^(−1) ((−1)/2)]−2[0+2sin^(−1) (−1)] = 2[(−√3)/( 2)+2 sin^(−1) ((−1)/2)]−2[2 sin^(−1) (−1)] = −√3+4 sin^(−1) ((−1)/2)−4 sin^(−1) (−1) Using sin–1 (–x) = – sin–1 x = −√3−4 sin^(−1) (1/2)+4 sin^(−1) (1) = −√3−4 ×𝜋/6+4×𝜋/2 = −√3−2𝜋/3+2𝜋 = −√3+4𝜋/3 Therefore, Area required = Area ACA’D + Area OADA’ = (4𝜋/3−√3) + ("–" √3 " + " 4𝜋/3) = 𝟖𝝅/𝟑−𝟐√𝟑 square units