Example 1 - Chapter 8 Class 12 Application of Integrals (Term 2)

Transcript

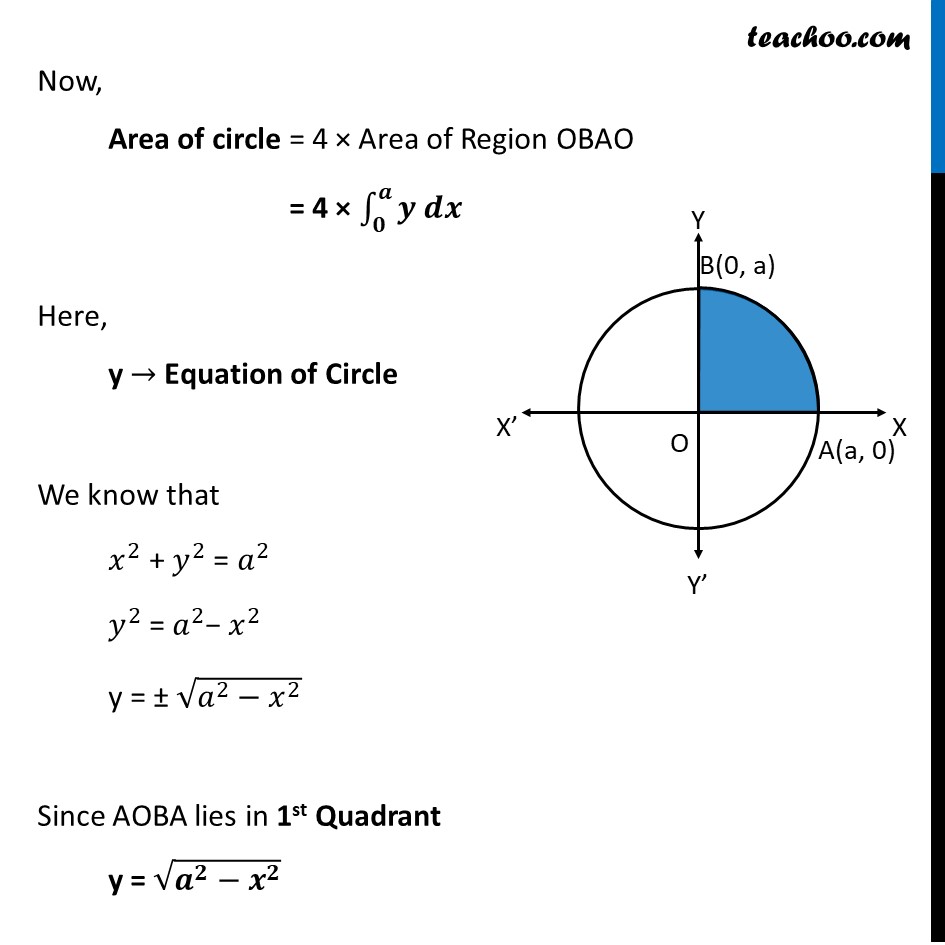
Example 1 Find the area enclosed by the circle 𝑥2 + 𝑦2 = 𝑎2 Drawing circle 𝑥^2 + 𝑦^2= 𝑎^2 Center = (0, 0) Radius = 𝑎 Hence OA = OB = Radius = 𝑎 A = (𝑎, 0) B = (0, 𝑎) Since Circle is symmetric about x-axis and y-axis Area of circle = 4 × Area of Region OBAO = 4 × ∫1_0^𝑎▒〖𝑦 𝑑𝑥〗 We know that 𝑥^2 + 𝑦^2 = 𝑎^2 𝑦^2 = 𝑎^2− 𝑥^2 y = ±√(𝑎^2−𝑥^2 ) Since AOBA lies in 1st Quadrant, Value of y is positive y = √(𝑎^2−𝑥^2 ) Now, Area of circle = 4 × ∫1_0^𝑎▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥〗 Using: √(𝑎^2−𝑥^2 )dx = 1/2 √(𝑎^2−𝑥^2 ) + 𝑎^2/2 〖"sin" 〗^(−1) 𝑥/𝑎 + c = 4[𝑥/2 √(𝑎^2−𝑥^2 )+𝑎^2/2 〖"sin" 〗^(−1) 𝑥/𝑎]_0^𝑎 = 4[(𝑎/2 √(𝑎^2−𝑎^2 )+𝑎^2/2 〖"sin" 〗^(−1) 𝑎/𝑎)−(0/2 √(𝑎^2−0)+0^2/2 〖"sin" 〗^(−1) (0))] = 4[0+𝑎^2/2 〖"sin" 〗^(−1) (1)−0−0] = 4 × 𝑎^2/2 〖"sin" 〗^(−1) (1) = 4 × 𝑎^2/2× 𝜋/2 = 𝝅𝒂^𝟐