



Area between 2 curves
Last updated at December 16, 2024 by Teachoo





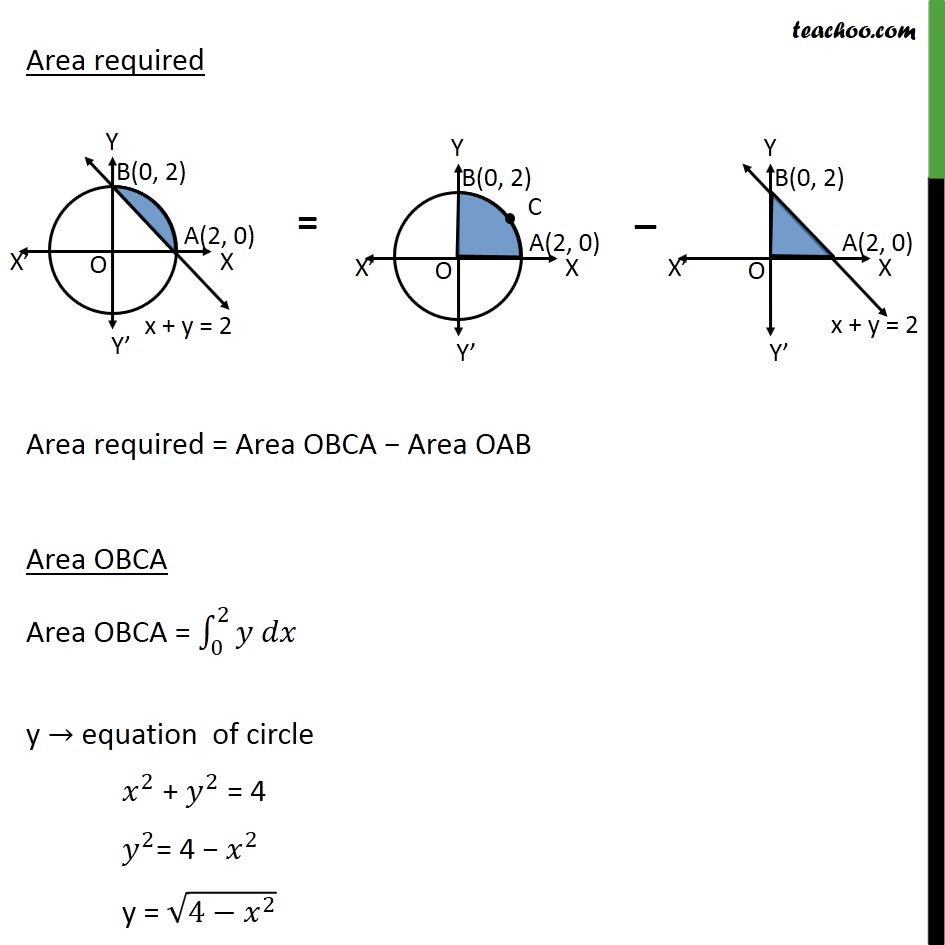
Transcript
Ex 8.2 , 6 Smaller area enclosed by the circle 𝑥2+𝑦2 =4 and the line 𝑥+𝑦=2 is (A) 2 (π – 2) (B) π – 2 (C) 2π – 1 (D) 2 (π + 2) Step 1: Drawing figure Circle is 𝑥2+𝑦2 =4 (𝑥−0)2+(𝑦−0)2 = 22 So, Center = (0, 0) & Radius = 2 Also, 𝑥+𝑦=2 passes through (0, 2) & (2, 0) Hence, intersecting points A = (2, 0) & B = (0, 2) Thus, Area required = Area OACB − AREA OAB = 𝜋 − 2 Thus, Option (B) is correct.