Question 2 - Area between 2 curves - Chapter 8 Class 12 Application of Integrals

Transcript

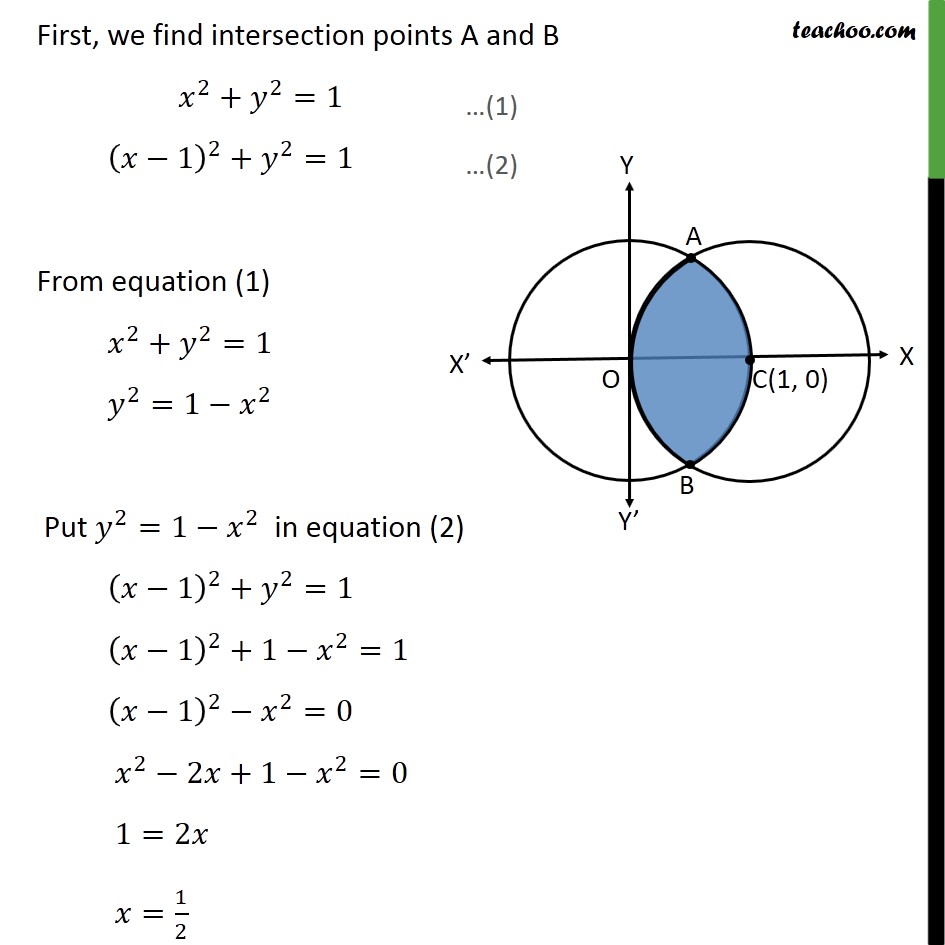
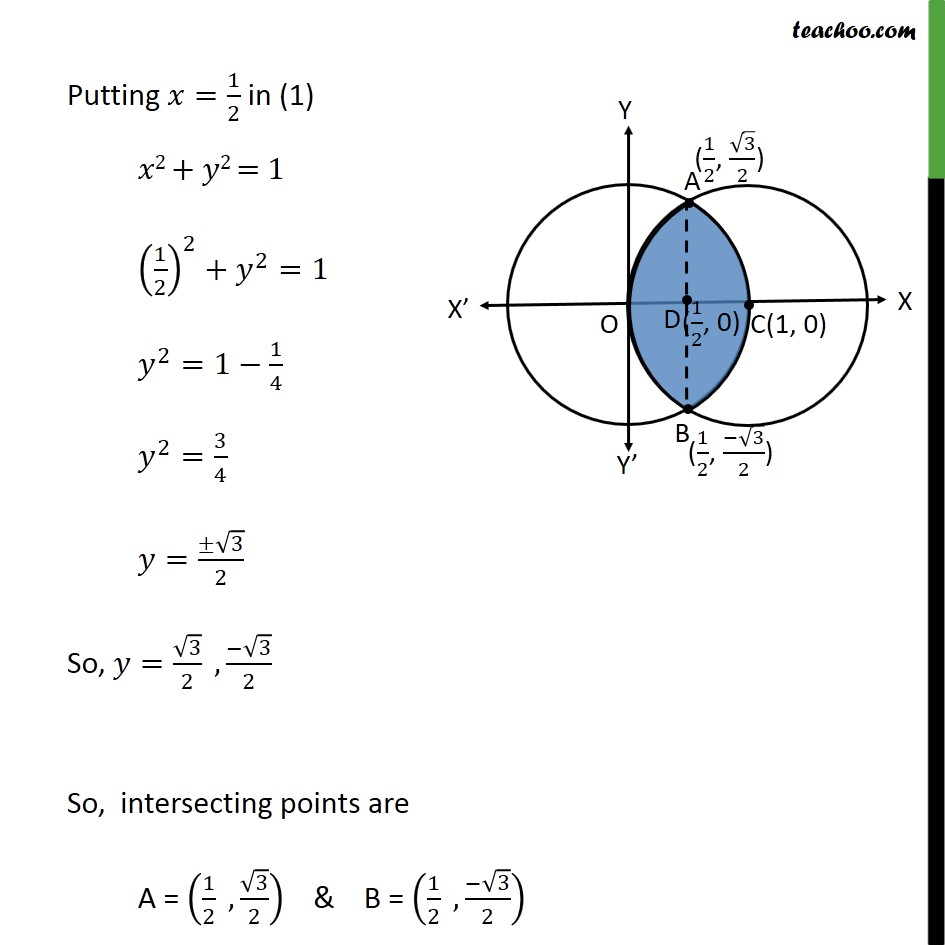
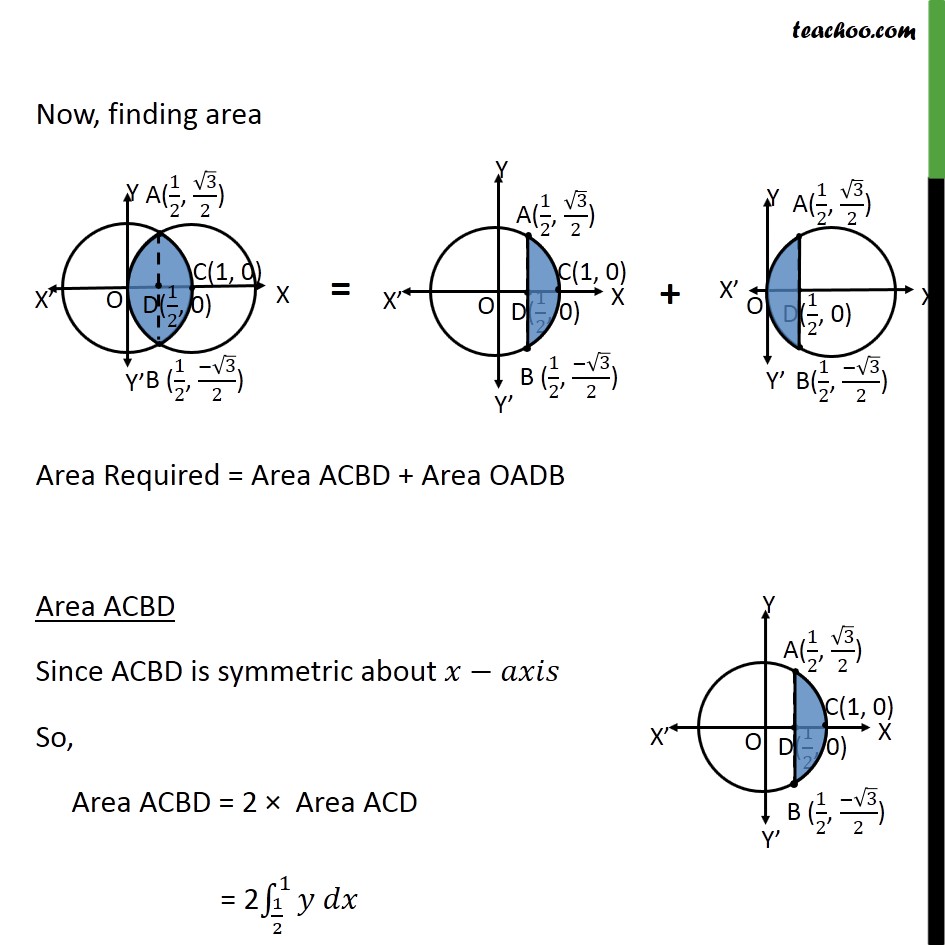
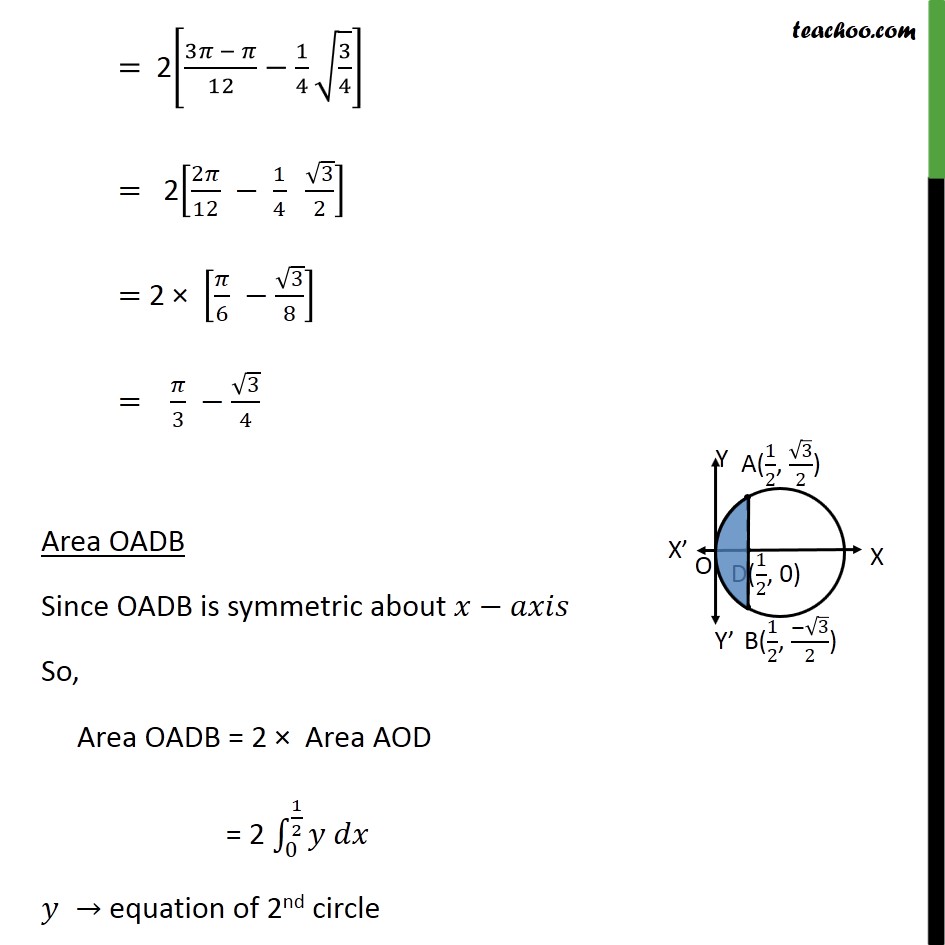
Ex 8.2 , 2 Find the area bounded by curves 𝑥 – 1﷯﷮2﷯ + 𝑦2=1 𝑎𝑛𝑑 𝑥2+𝑦2=1 First we find center and radius of both circles Drawing figure Area required = Area OACB First, we find intersection points A and B 𝑥﷮2﷯+ 𝑦﷮2﷯=1 𝑥−1﷯﷮2﷯+ 𝑦﷮2﷯=1 From equation (1) 𝑥﷮2﷯+ 𝑦﷮2﷯=1 𝑦﷮2﷯=1− 𝑥﷮2﷯ Put 𝑦﷮2﷯=1− 𝑥﷮2﷯ in equation (2) 𝑥−1﷯﷮2﷯+ 𝑦﷮2﷯=1 𝑥−1﷯﷮2﷯+1− 𝑥﷮2﷯=1 𝑥−1﷯﷮2﷯− 𝑥﷮2﷯=0 𝑥﷮2﷯−2𝑥+1− 𝑥﷮2﷯=0 1=2𝑥 𝑥= 1﷮2﷯ Putting 𝑥= 1﷮2﷯ in (1) 𝑥2 + 𝑦2 = 1 1﷮2﷯﷯﷮2﷯+ 𝑦﷮2﷯=1 𝑦﷮2﷯=1− 1﷮4﷯ 𝑦﷮2﷯= 3﷮4﷯ 𝑦= ± ﷮3﷯﷮2﷯ So, 𝑦= ﷮3﷯﷮2﷯ , − ﷮3﷯﷮2﷯ So, intersecting points are A = 1﷮2﷯ , ﷮3﷯﷮2﷯﷯ & B = 1﷮2﷯ , − ﷮3﷯﷮2﷯﷯ Now, finding area Area Required = Area ACBD + Area OADB Area ACBD Since ACBD is symmetric about 𝑥−𝑎𝑥𝑖𝑠 So, Area ACBD = 2 × Area ACD = 2 1﷮2﷯﷮1﷮𝑦 𝑑𝑥﷯ 𝑦 → equation of 1st circle 𝑥﷮2﷯+ 𝑦﷮2﷯=1 𝑦﷮2﷯=1− 𝑥﷮2﷯ 𝑦=± ﷮1− 𝑥﷮2﷯﷯ Since Area ACD is in 1st quadrant, we take positive value So, 𝑦= ﷮1− 𝑥﷮2﷯﷯ Hence, Area ACBD = 2 1﷮2﷯﷮1﷮𝑦 𝑑𝑥﷯ = 2 1﷮2﷯﷮1﷮ ﷮1− 𝑥﷮2﷯﷯﷯ 𝑑𝑥 = 2 1﷮2﷯﷮1﷮ ﷮ 1﷮2﷯− 𝑥﷮2﷯﷯﷯ 𝑑𝑥 = 2 𝑥﷮2﷯ ﷮1− 𝑥﷮2﷯﷯+ 1﷮2﷯﷮2﷯ sin﷮−1﷯﷮ 𝑥﷮1﷯﷯﷯﷮ 1﷮2﷯﷮1﷯ = 2 𝑥﷮2﷯ ﷮1− 𝑥﷮2﷯﷯+ 1﷮2﷯ sin﷮−1﷯﷮𝑥﷯﷯﷮ 1﷮2﷯﷮1﷯ = 2 1﷮2﷯ ﷮1−1﷯+ 1﷮2﷯ sin﷮−1﷯1﷯− 1﷮2﷯﷯﷮2﷯ ﷮1− 1﷮2﷯﷯﷮2﷯﷯+ 1﷮2﷯ sin﷮−1﷯﷮ 1﷮2﷯﷯﷯﷯﷯ = 2 1﷮2﷯ ﷮0﷯+ 1﷮2﷯ × 𝜋﷮2﷯− 1﷮4﷯ ﷮1− 1﷮4﷯﷯ − 1﷮2﷯ 𝜋﷮6﷯﷯ = 2 𝜋﷮4﷯− 𝜋﷮12﷯− 1﷮4﷯ ﷮ 4 − 1﷮4﷯﷯﷯ = 2 3𝜋 − 𝜋﷮12﷯− 1﷮4﷯ ﷮ 3﷮4﷯﷯﷯ = 2 2𝜋﷮12﷯ − 1﷮4﷯ ﷮3﷯﷮2﷯﷯ = 2 × 𝜋﷮6﷯ − ﷮3﷯﷮8﷯﷯ = 𝜋﷮3﷯ − ﷮3﷯﷮4﷯ Area OADB Since OADB is symmetric about 𝑥−𝑎𝑥𝑖𝑠 So, Area OADB = 2 × Area AOD = 2 0﷮ 1﷮2﷯﷮𝑦 𝑑𝑥﷯ 𝑦 → equation of 2nd circle 𝑥−1﷯﷮2﷯+ 𝑦﷮2﷯=1 𝑦﷮2﷯=1− 𝑥−1﷯﷮2﷯ 𝑦=± ﷮1− 𝑥−1﷯﷮2﷯﷯ Since Area AOD is in 1st quadrant, we take positive value So, 𝑦= ﷮1− 𝑥−1﷯﷮2﷯﷯ Hence, Area OADB = 2 0﷮ 1﷮2﷯﷮𝑦 𝑑𝑥﷯ = 2 0﷮ 1﷮2﷯﷮ ﷮1− 𝑥−1﷯﷮2﷯﷯﷯ 𝑑𝑥 Putting t = 𝑥−1 Diff w.r.t 𝑥 𝑑𝑡﷮𝑑𝑥﷯=1 𝑑𝑡=𝑑𝑥 So, = 2 0﷮ 1﷮2﷯﷮ ﷮1− 𝑥−1﷯﷮2﷯﷯ 𝑑𝑥﷯ =2 −1﷮ −1﷮ 2﷯﷮ ﷮1− 𝑡﷮2﷯﷯ 𝑑𝑡﷯ =2 𝑡﷮2﷯ ﷮1− 𝑡﷮2﷯﷯+ 1﷮2﷯﷮2﷯ sin﷮−1﷯﷮ 𝑡﷮1﷯﷯﷯﷮−1﷮ −1﷮ 2﷯﷯ =2 −1﷮ 2﷯﷯﷮2﷯ ﷮1− −1﷮ 2﷯﷯﷮2﷯﷯+ 1﷮2﷯﷮2﷯ sin﷮−1﷯﷮ −1﷮ 2﷯﷯﷮1﷯﷯− −1﷯﷮2﷯ ﷮1− −1﷯﷮2﷯﷯+ 1﷮2﷯ sin﷮−1﷯﷮ −1﷯﷯﷯﷯ = 2 −1﷮ 2﷯ ﷮1− 1﷮4﷯﷯+ 1﷮2﷯ × −𝜋﷮6﷯﷯+ ﷮0﷯− 1﷮2﷯ −𝜋﷮ 2﷯﷯﷯ = 2 −1﷮ 4﷯ ﷮ 3﷮4﷯﷯− 𝜋﷮12﷯+ 𝜋﷮4﷯﷯ = 2 − ﷮3﷯﷮4 ×2﷯+ 𝜋 ﷮4﷯− 𝜋﷮12﷯﷯ = 2 − ﷮3﷯﷮ 8﷯+ 3𝜋 − 𝜋﷮12﷯﷯ = 2 − ﷮3﷯﷮8﷯+ 2𝜋﷮12﷯﷯ = − ﷮3﷯﷮4﷯+ 𝜋﷮3﷯ Area Required = Area ACBD + Area OADB = 𝜋 ﷮3﷯− ﷮3﷯﷮ 4﷯− ﷮3﷯﷮ 4﷯+ 𝜋﷮3﷯ = 𝟐𝝅﷮𝟑﷯− ﷮𝟑﷯﷮ 𝟐﷯