Ex 8.1, 3 (MCQ) - Chapter 8 Class 12 Application of Integrals

Transcript

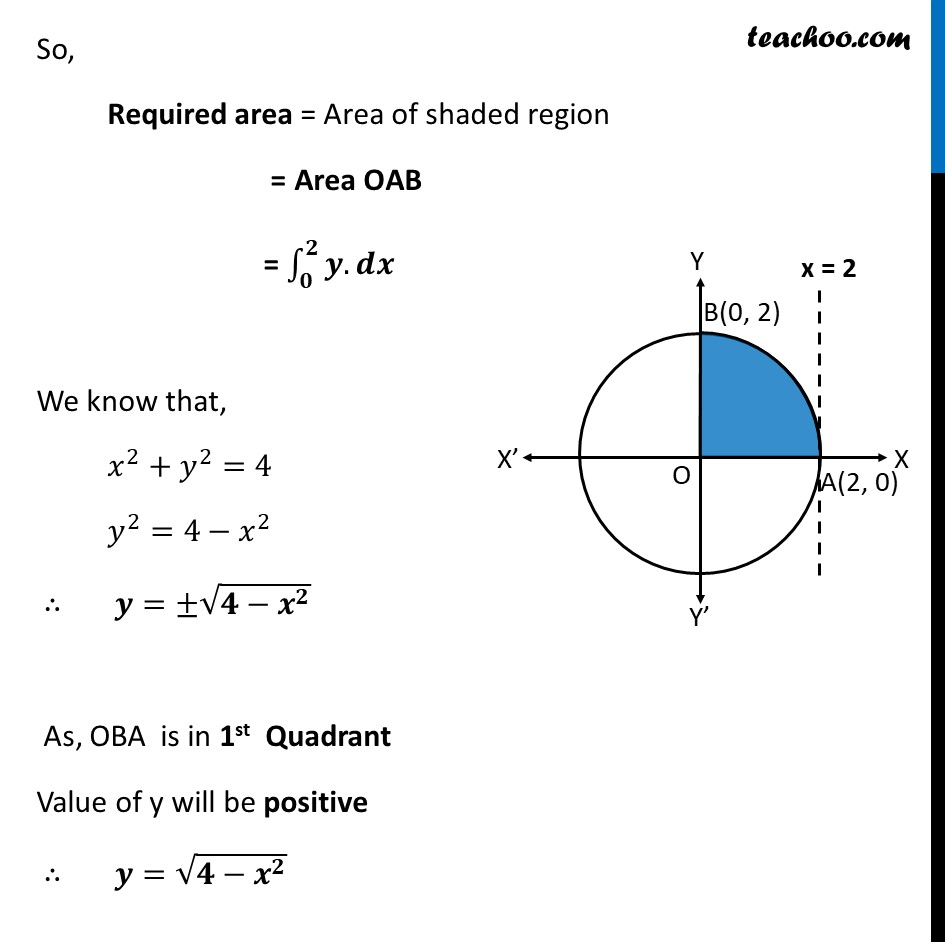
Ex 8.1, 3 Area lying in the first quadrant and bounded by the circle 𝑥2+𝑦2=4 and the lines 𝑥 = 0 and 𝑥 = 2 is (A) π (B) 𝜋/2 (C) 𝜋/3 (D) 𝜋/4Given Equation of Circle :- 𝑥^2+𝑦^2=4 𝒙^𝟐+𝒚^𝟐=(𝟐)^𝟐 ∴ Radius = 𝒓=𝟐 Now, Line 𝒙=𝟎 is y-axis & Line x = 2 passes through point A (𝟐 , 𝟎) So, Required area = Area of shaded region = Area OAB = ∫_𝟎^𝟐▒〖𝒚.𝒅𝒙〗 We know that, 𝑥^2+𝑦^2=4 𝑦^2=4−𝑥^2 ∴ 𝒚=±√(𝟒−𝒙^𝟐 ) As, OBA is in 1st Quadrant Value of y will be positive ∴ 𝒚=√(𝟒−𝒙^𝟐 ) Now, Required area = ∫_0^2▒〖𝑦.𝑑𝑥〗 = ∫_0^2▒〖√(4−𝑥^2 ) 𝑑𝑥〗 = ∫_𝟎^𝟐▒〖√((𝟐)^𝟐−𝒙^𝟐 ) 𝒅𝒙〗 = [(𝑥 )/2 √((2)^2−𝑥^2 )+2 sin^(−1)⁡〖𝑥/2 〗 ]_0^2 = [2/2 √((2)^2−2^2 )+2 sin^(−1)⁡〖2/2 〗−0/2 √((2)^2−(0)^2 )−2 sin^(−1)⁡〖0/2〗 ] = [0+2 sin^(−1)⁡〖(1)−0√4−2 sin^(−1)⁡(0) 〗 ] = 2 sin^(−1)⁡〖(1)−2 sin^(−1)⁡(0) 〗−0 It is of form √(𝒂^𝟐−𝒙^𝟐 ) 𝒅𝒙=1/2 𝑥√(𝑎^2−𝑥^2 )+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖 𝑥/𝑎+𝑐〗 Replacing a by 2 , we get = 2[〖𝒔𝒊𝒏〗^(−𝟏)⁡〖(𝟏)−〖𝒔𝒊𝒏〗^(−𝟏)⁡(𝟎) 〗 ] = 2[𝜋/2−0] = 2 . 𝜋/2 = π Therefore, Area Required = π square units So, the correct answer is (a)