

Area between curve and line
Area between curve and line
Last updated at December 16, 2024 by Teachoo








Transcript
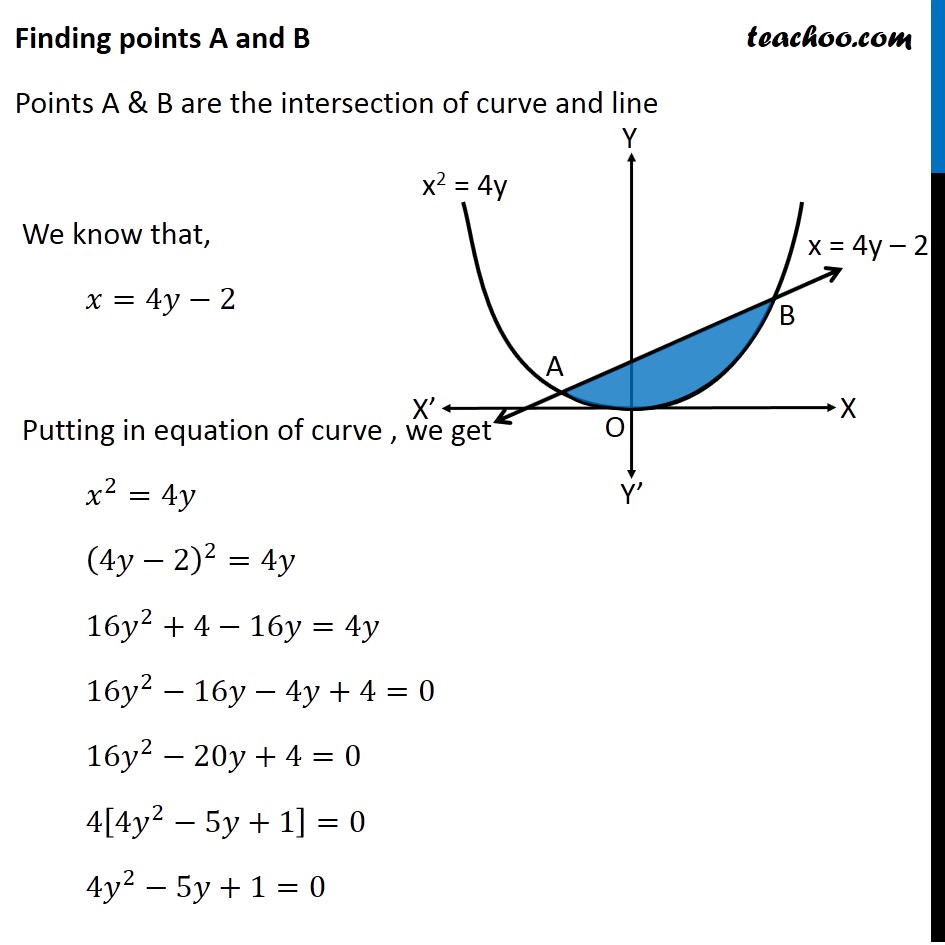
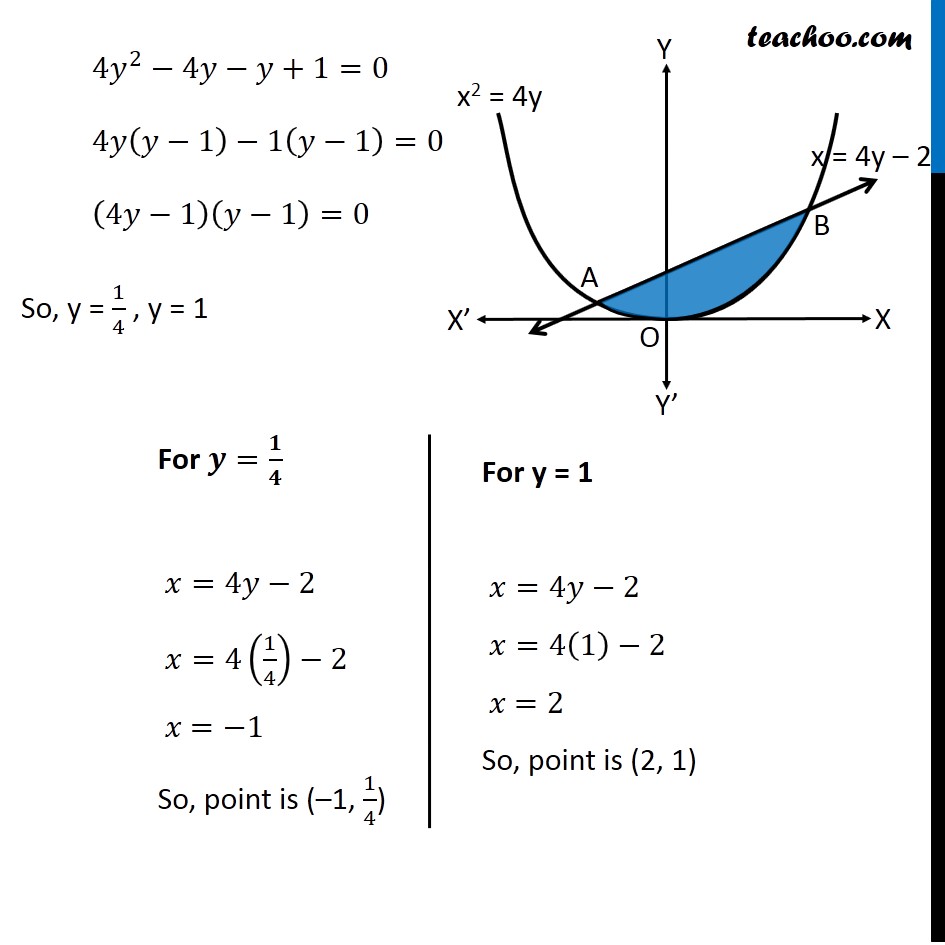
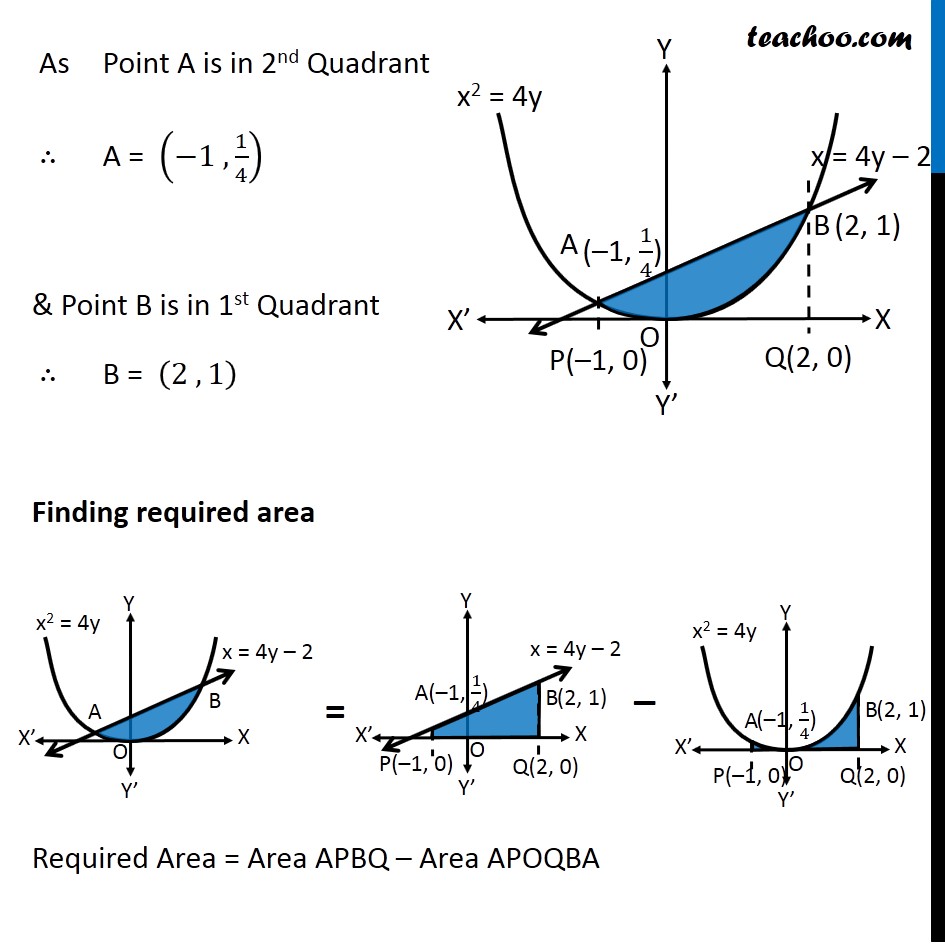
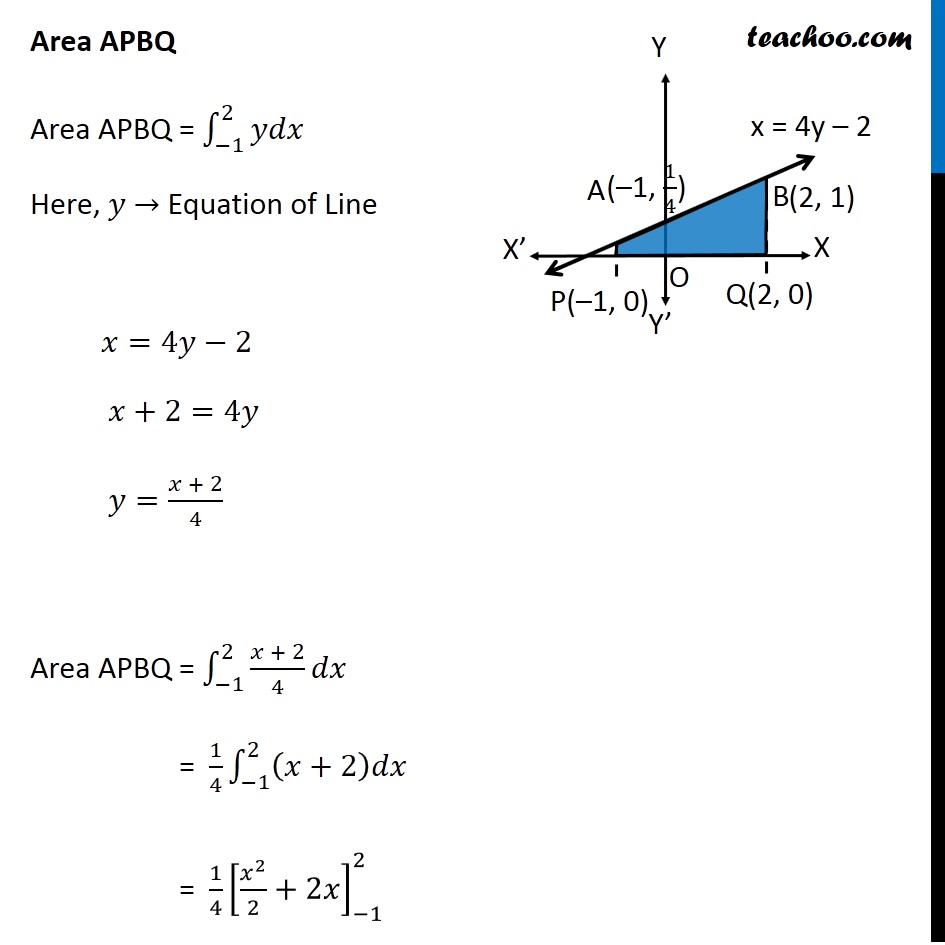
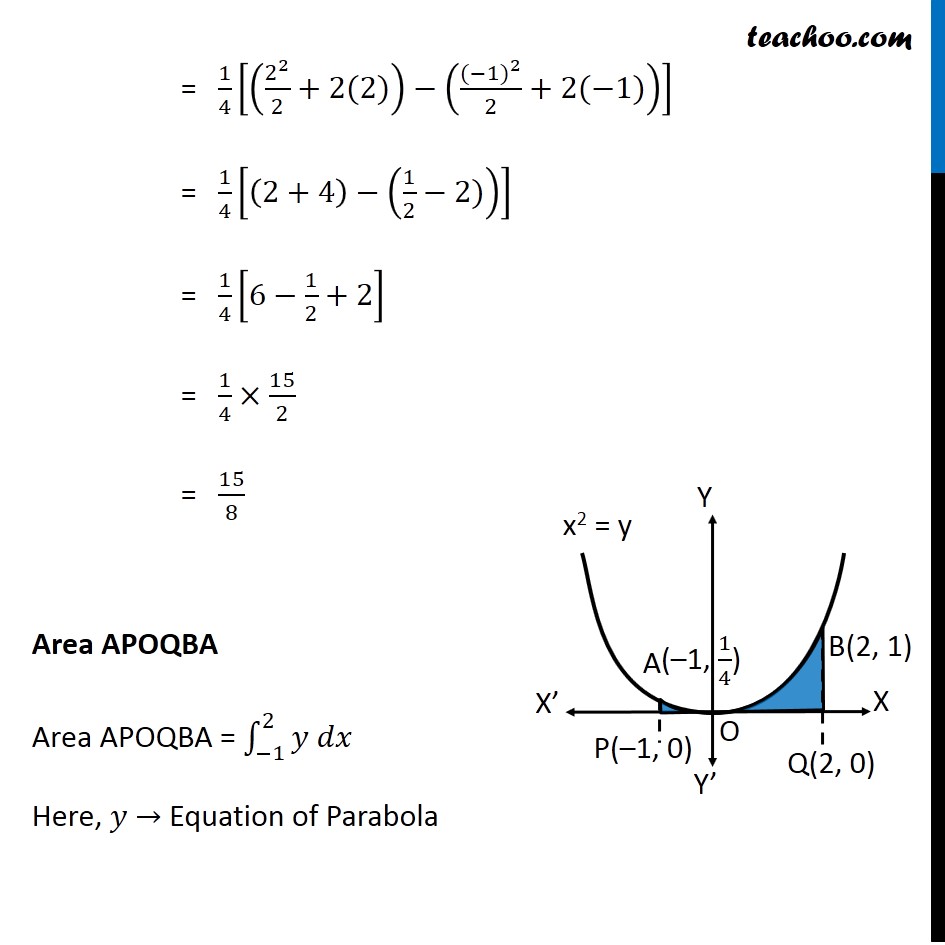
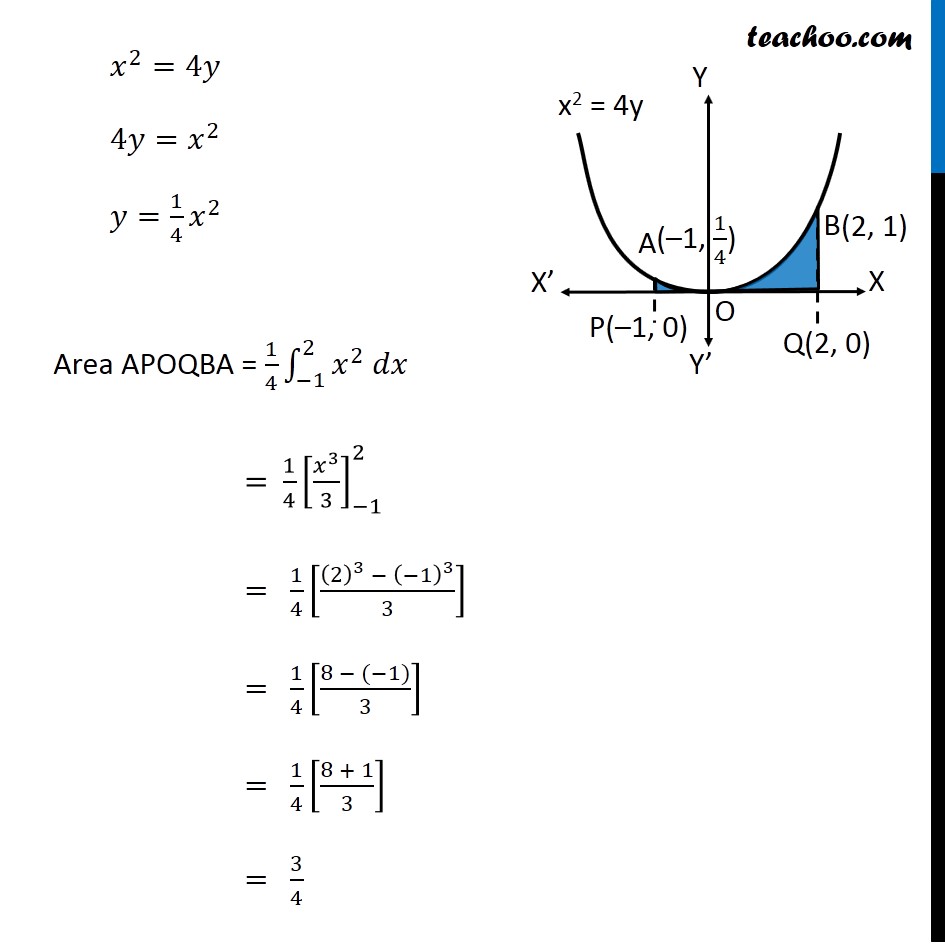
Question 8 Find the area bounded by the curve 𝑥2=4𝑦 and the line 𝑥=4𝑦 – 2 Here, 𝑥2=4𝑦 is a parabola And, x = 4y – 2 is a line which intersects the parabola at points A and B We need to find Area of shaded region First we find Points A and B Finding points A and B Points A & B are the intersection of curve and line We know that, 𝑥=4𝑦−2 Putting in equation of curve , we get 𝑥^2=4𝑦 (4𝑦−2)^2=4𝑦 16𝑦^2+4−16𝑦=4𝑦 16𝑦^2−16𝑦−4𝑦+4=0 16𝑦^2−20𝑦+4=0 4[4𝑦^2−5𝑦+1]=0 4𝑦^2−5𝑦+1=0 4𝑦^2−4𝑦−𝑦+1=0 4𝑦(𝑦−1)−1(𝑦−1)=0 (4𝑦−1)(𝑦−1)=0 So, y = 1/4 , y = 1 For 𝒚=𝟏/𝟒 𝑥=4𝑦−2 𝑥=4(1/4)−2 𝑥 =−1 So, point is (–1, 1/4) For y = 1 𝑥=4𝑦−2 𝑥=4(1)−2 𝑥 =2 So, point is (2, 1) As Point A is in 2nd Quadrant ∴ A = (−1 , 1/4) & Point B is in 1st Quadrant ∴ B = (2 , 1) Finding required area Required Area = Area APBQ – Area APOQBA Area APBQ Area APBQ = ∫_(−1)^2▒𝑦𝑑𝑥 Here, 𝑦 → Equation of Line 𝑥=4𝑦−2 𝑥+2=4𝑦 𝑦=(𝑥 + 2)/4 Area APBQ = ∫_(−1)^2▒(𝑥 + 2)/4 𝑑𝑥 = 1/4 ∫1_(−1)^2▒(𝑥+2)𝑑𝑥 = 1/4 [𝑥^2/2+2𝑥]_(−1)^2 = 1/4 [(2^2/2+2(2))−(〖(−1)〗^2/2+2(−1))] = 1/4 [(2+4)−(1/2−2))] = 1/4 [6−1/2+2] = 1/4×15/2 = 15/8 Area APOQBA Area APOQBA = ∫_(−1)^2▒〖𝑦 𝑑𝑥〗 Here, 𝑦 → Equation of Parabola 𝑥^2=4𝑦 4𝑦=𝑥^2 𝑦=1/4 𝑥^2 Area APOQBA = 1/4 ∫1_(−1)^2▒〖𝑥^2 𝑑𝑥〗 = 1/4 [𝑥^3/3]_(−1)^2 = 1/4 [((2)^3 − (−1)^3)/3] = 1/4 [(8 − (−1))/3] = 1/4 [(8 + 1)/3] = 3/4 Now, Required Area = Area APBQ – Area APOQBA = 15/8 – 3/4 " = " (15 − 6)/8 = 9/8 ∴ Required Area = 𝟗/𝟖 Square units