

Last updated at April 16, 2024 by Teachoo




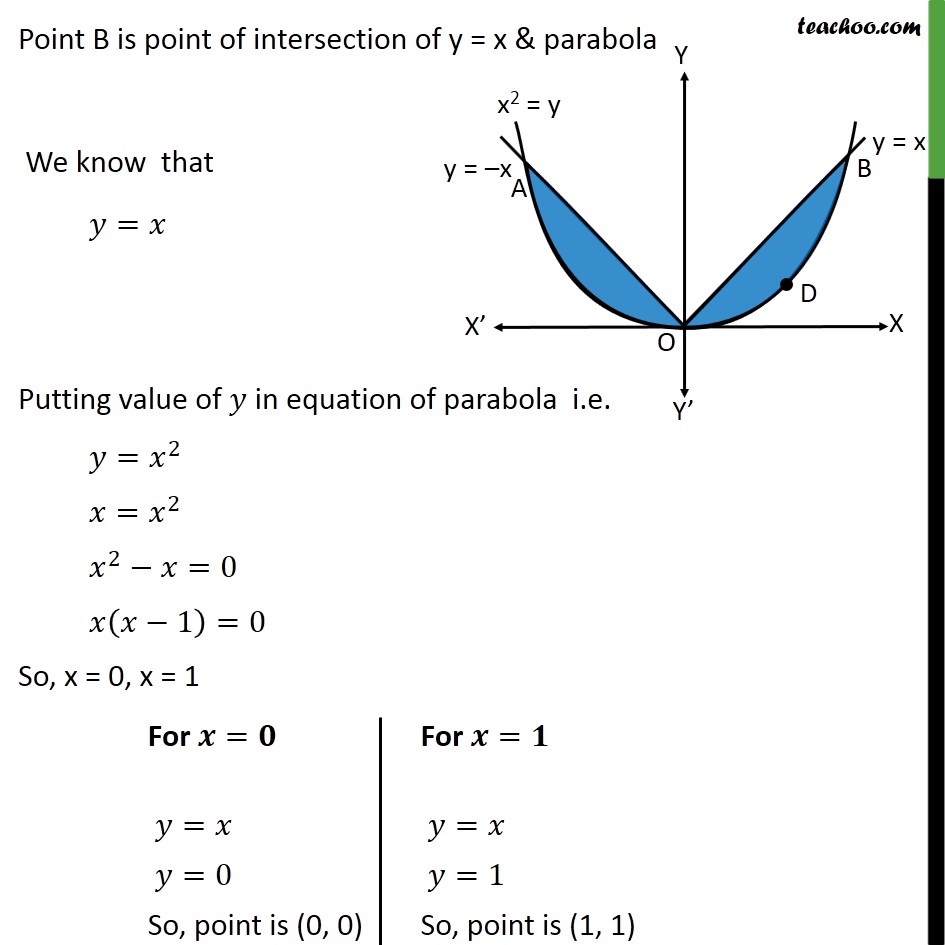
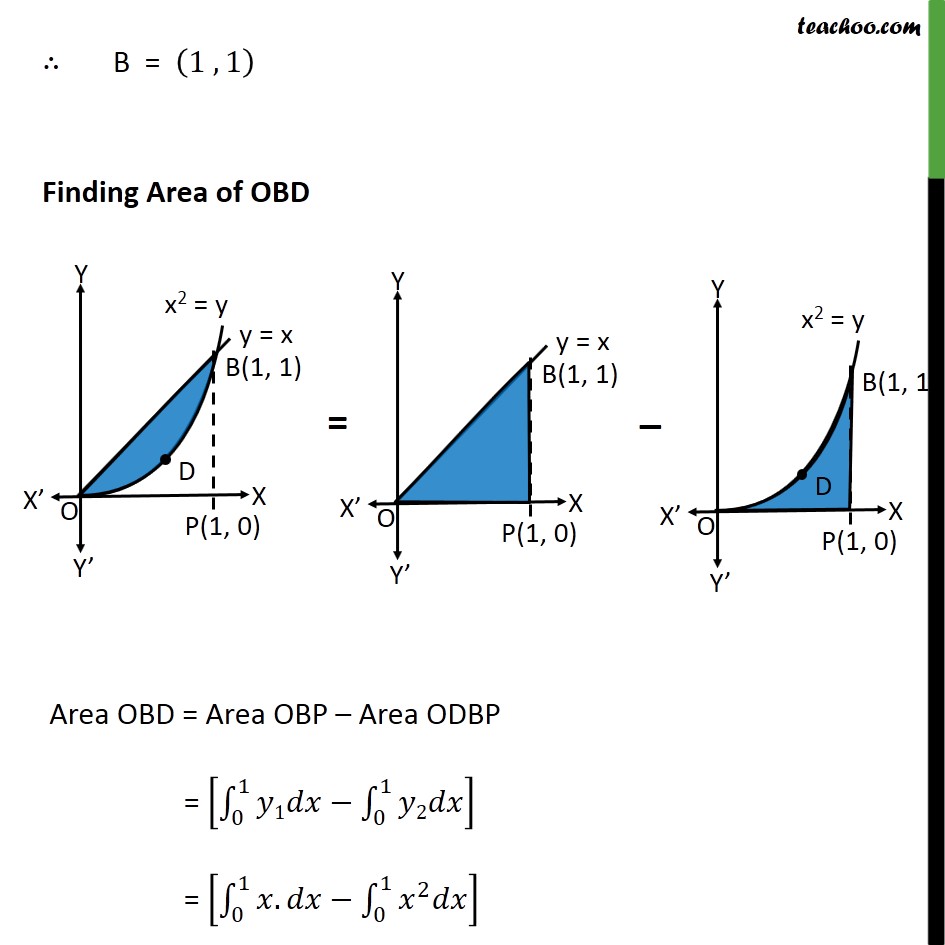
Question 7 Find the area of the region bounded by the parabola = 2 and = We know = & , <0 & , 0 Let OA represent the line = & OB represent the line = Since parabola is symmetric about its axis, x2 = y is symmetric about y axis Area of shaded region = 2 (Area of OBD) First, we find Point B, Point B is point of intersection of y = x & parabola We know that = Putting value of in equation of parabola i.e. = 2 = 2 2 =0 1 =0 So, x = 0, x = 1 B = 1 , 1 Finding Area of OBD Area OBD = Area OBP Area ODBP = 0 1 1 0 1 2 = 0 1 . 0 1 2 Area of shaded region = 2 (Area of OBD) = 2 0 1 . 0 1 2 = 2 2 2 0 1 3 3 0 1 = 2 1 0 2 1 0 3 = 2 1 2 1 3 = 2 3 2 6 = 1 3 Required Area = square units