You are here
Question 5 - Area bounded by curve and horizontal or vertical line - Chapter 8 Class 12 Application of Integrals
Last updated at Dec. 16, 2024 by Teachoo
Area bounded by curve and horizontal or vertical line
Chapter 8 Class 12 Application of Integrals
Concept wise
- Area under curve
-
Area bounded by curve and horizontal or vertical line
- Area between curve and line
- Area between curve and curve
Transcript
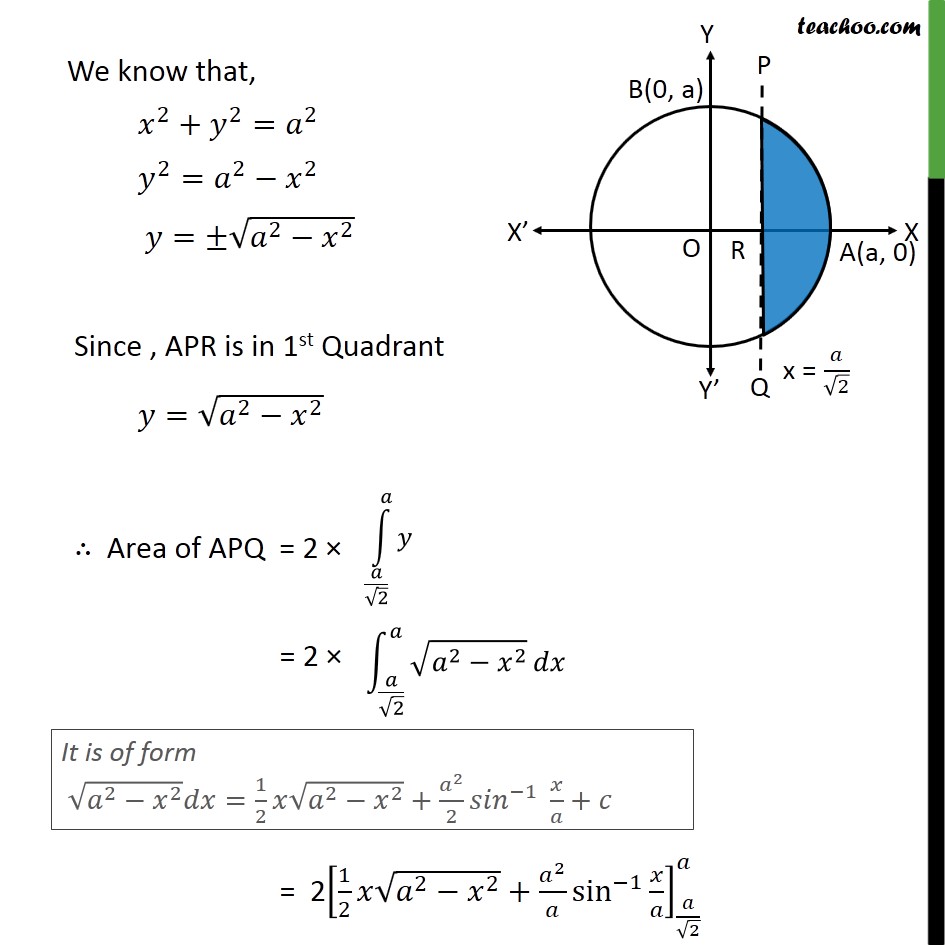
Question 5 Find the area of the smaller part of the circle 2+ 2= 2 cut off by the line = 2 . Equation of Given Circle is 2 + 2 = 2 Radius , = So, a is positive = 2 will lie on positive side of x-axis Let PQ represent the line = 2 We have to find Area of APQ Area APQ = 2 Area APR = 2 We know that, 2 + 2 = 2 2 = 2 2 = 2 2 Since , APR is in 1st Quadrant = 2 2 Area of APQ = 2 = 2 = 2 1 2 2 2 + 2 sin 1 2 = 2 2 2 2 + 2 2 sin 1 2 2 2 2 2 2 2 sin 1 2 = 2 0+ 2 2 sin 1 1 2 2 2 2 2 2 2 sin 1 1 2 = 2 2 2 1 1 2 2 sin 1 1 2 2 2 2 2 2 2 = 2 2 2 sin 1 1 sin 1 1 2 2 2 2 2 = 2 2 2 2 4 2 2 2 = 2 2 2 2 4 2 2.2 = 2 2 2 4 2 4 = 2 2 4 2 1 = 2 2 2 1 Required Area = Square units
