Ex 8.1, 1 - Chapter 8 Class 12 Application of Integrals

Transcript

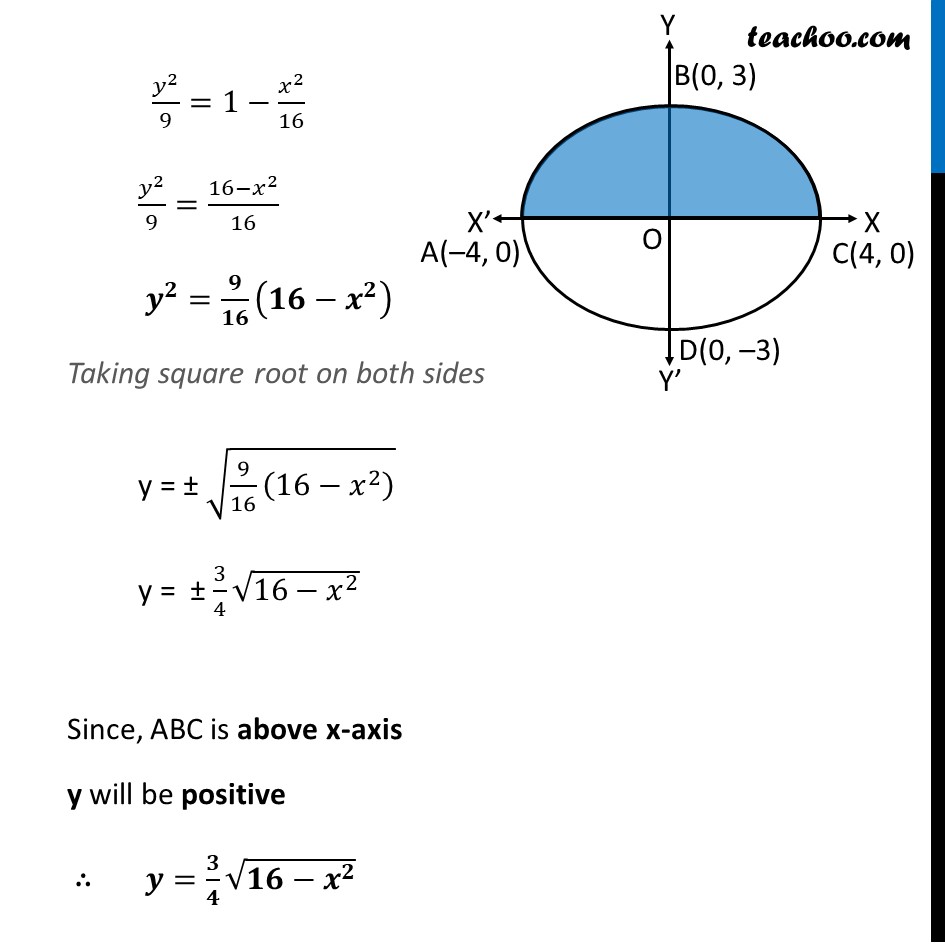
Ex 8.1, 1 Find the area of the region bounded by the ellipse 𝑥^2/16+𝑦^2/9=1Equation Of Given Ellipse is 𝑥^2/16+𝑦^2/9=1 𝒙^𝟐/(𝟒)^𝟐 +𝒚^𝟐/(𝟑)^𝟐 =𝟏 Area of ellipse = Area of ABCD = 2 × [Area Of ABC] = 2 × ∫_(−𝟒)^𝟒▒〖𝒚.〗 𝒅𝒙 Finding y We know that 𝑥^2/16+𝑦^2/9=1 𝑦^2/9=1−𝑥^2/16 𝑦^2/9=(16−𝑥^2)/16 𝒚^𝟐=𝟗/𝟏𝟔 (𝟏𝟔−𝒙^𝟐 ) Taking square root on both sides y = ± √(9/16 (16−𝑥^2 ) ) y = ± 3/4 √(16−𝑥^2 ) Since, ABC is above x-axis y will be positive ∴ 𝒚=𝟑/𝟒 √(𝟏𝟔−𝒙^𝟐 ) Now, Area of ellipse = 2 × ∫_(−4)^4▒〖𝑦.〗 𝑑𝑥 = 2 × ∫_(−𝟒)^𝟒▒〖 𝟑/𝟒 √(𝟏𝟔−𝒙^𝟐 )〗 𝒅𝒙 = 2 × 3/4 ∫_(−4)^4▒√(16−𝑥^2 ) 𝑑𝑥 = 𝟑/𝟐 ∫_(−𝟒)^𝟒▒√((𝟒)^𝟐−𝒙^𝟐 ) 𝒅𝒙 It is of form √(𝑎^2−𝑥^2 ) 𝑑𝑥=1/2 𝑥√(𝑎^2−𝑥^2 )+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖 𝑥/𝑎+𝑐〗 Replacing a by 4 we get = 3/2 [𝑥/2 √((4)^2−𝑥^2 )+(4)^2/2 sin^(−1)⁡〖 𝑥/4〗 ]_(−4)^4 = 3/2 [4/2 √((4)^2−(4)^2 )−((−4))/2 √((4)^2−(−4)^2 )+16/2 〖 sin〗^(−1)⁡〖(4/4)−16/2〗 sin^(−1) ((−4)/4)] = 3/2 [2(0)+2(0)+8 〖sin^(−1) (1)〗⁡〖− 8 sin^(−1)⁡(−1) 〗 ] = 3/2 [0+8 sin^(−1)⁡〖(1)−8 〖𝒔𝒊𝒏〗^(−𝟏)⁡(−𝟏) 〗 ] = 3/2 [8 sin^(−1)⁡〖(1)−8(−〖𝒔𝒊𝒏〗^(−𝟏)⁡(𝟏))〗 ] = 3/2 [8 sin^(−1)⁡〖(1)+8 sin^(−1)⁡(1) 〗 ] = 3/2 × 16 〖𝒔𝒊𝒏〗^(−𝟏)⁡(𝟏) = 3/2 × 16 × 𝝅/𝟐 = 3 × 8 × 𝜋/2 = 12π ∴ Area of Ellipse = 12π Square units