Misc 7 - Chapter 4 Class 12 Determinants (Important Question)

Transcript

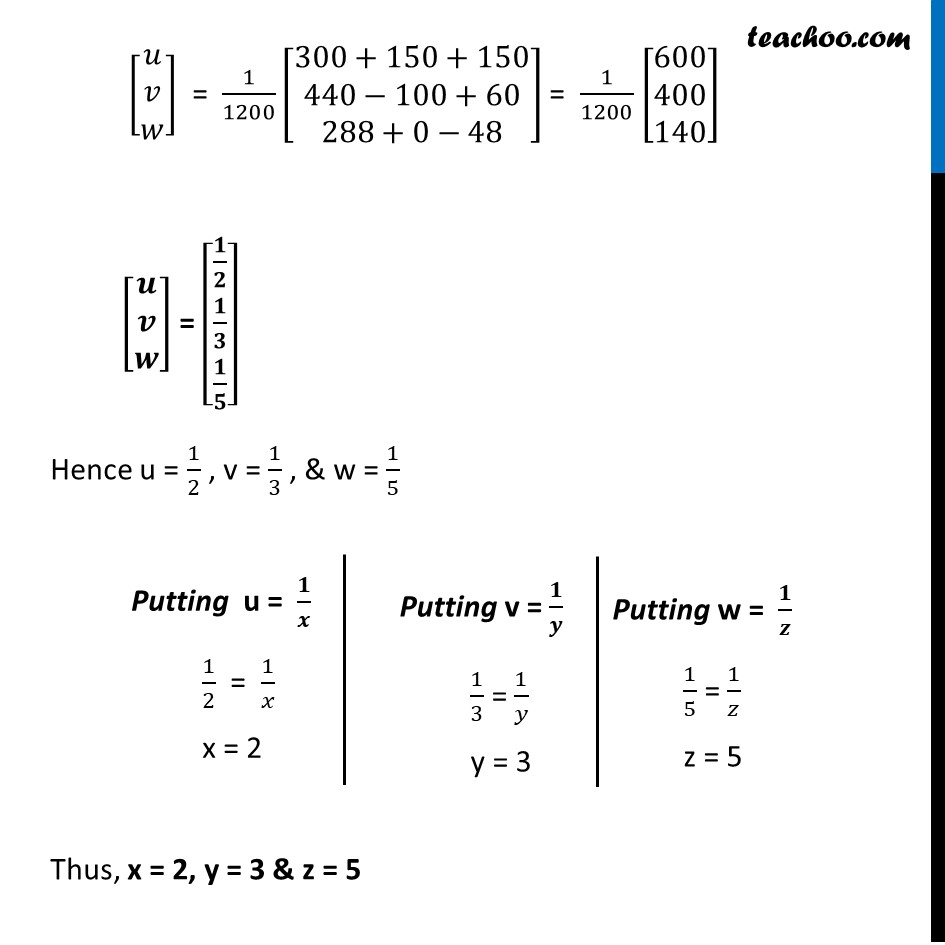
Misc 7 Solve the system of the following equations 2/x + 3/y + 10/z = 4 4/x + 6/y + 5/z = 1 6/x + 9/y + 20/z = 2 The system of equations are 2/x + 3/y + 10/z = 4 4/x + 6/y + 5/z = 1 6/x + 9/y + 20/z = 2 Now let 𝟏/𝒙 = u , 𝟏/𝒚 = v , & 𝟏/𝒛 = w The system of equations become 2u + 3v + 10w = 4 4u – 6v + 5w = 1 6u + 9v – 20w = 2 Writing equation as AX = B [■8(2&3&10@4&−6&5@6&9&−20)] [■8(𝑢@𝑣@𝑤)] = [■8(4@1@2)] Hence A = [■8(2&3&10@4&−6&5@6&9&−20)] , X = [■8(𝑢@𝑣@𝑤)] & B = [■8(4@1@2)] Calculating |A| |A| = |■8(2&3&10@4&−6&5@6&9&−20)| = 2 |■8(−6&5@9&−20)| – 3 |■8(4&5@6&−20)| + 10 |■8(4&−6@6&9)| = 2 (120 – 45) –3 (–80 – 30) + 10 ( 36 + 36) = 2 (75) –3 (–110) + 10 (72) = 150 + 330 + 720 = 1200 ∴ |A|≠ 0 So, the system of equation is consistent & has a unique solution Now, AX = B X = A-1 B Calculating A-1 Now, A-1 = 1/(|A|) adj (A) adj (A) = [■8(A11&A12&A13@A21&A22&A23@A31&A32&A33)]^′ = [■8(A11&A21&A31@A12&A22&A32@A13&A23&A33)] A = [■8(2&3&10@4&−6&5@6&9&−20)] M11 = |■8(−6&5@9&−20)| = 120 – 45 = 75 M12 = |■8(4&5@6&−20)| = (–80 – 30) = –110 M13 = |■8(4&−6@6&9)| = 36 –36 = 72 M21 = |■8(3&10@9&−20)| = −60 – 90 = –150 M22 = |■8(2&10@6&−20)| = –40 – 60 = –100 M23 = |■8(2&3@6&9)| = 18 – 18 = 0 M31 = |■8(3&10@−6&5)| = 15 + 60 = 75 M32 = |■8(2&10@4&5)| = 10 – 40 = –30 M33 = |■8(2&3@4&−6)| = –12 – 12 = –24 Now, A11 = 〖"(–1)" 〗^(1+1) M11 = (–1)2 . 75 = 75 A12 = 〖"(–1)" 〗^"1+2" M12 = 〖"(–1)" 〗^3 . (–110) = 110 A13 = 〖(−1)〗^(1+3) M13 = 〖(−1)〗^4 . (72) = 72 A21 = 〖(−1)〗^(2+1) M21 = 〖(−1)〗^3 . (–150) = 150 A22 = 〖(−1)〗^(2+2) M22 = (–1)4 . (–100) = –100 A23 = 〖(−1)〗^(2+3). M23 = 〖(−1)〗^5. 0 = 0 A31 = 〖(−1)〗^(3+1). M31 = 〖(−1)〗^4 . 75 = 75 A32 = 〖(−1)〗^(3+2) . M32 = 〖(−1)〗^5. (–30) = 30 A33 = 〖(−1)〗^(3+3) . M33 = (–1)6 . –24 = –24 Thus, adj A = [■8(75&150&75@110&−110&30@72&0&−24)] Now, A-1 = 1/(|A|) adj A A-1 = 𝟏/𝟏𝟐𝟎𝟎 [■8(𝟕𝟓&𝟏𝟓𝟎&𝟕𝟓@𝟏𝟏𝟎&−𝟏𝟏𝟎&𝟑𝟎@𝟕𝟐&𝟎&−𝟐𝟒)] Also, X = A−1 B Putting Values [■8(𝑢@𝑣@𝑤)]= 1/1200 [■8(75&150&75@110&−110&30@72&0&−24)] [■8(4@1@2)] [■8(𝑢@𝑣@𝑤)]= 1/1200 [■8(75(4)+150(1)+75(4)@110(4)+(−110)(1)+30(1)@72(4)+0(1)+(−24)2)] [■8(𝑢@𝑣@𝑤)] = 1/1200 [■8(300+150+150@440−100+60@288+0−48)] = 1/1200 [■8(600@400@140)] [■8(𝒖@𝒗@𝒘)] = [■8(𝟏/𝟐@𝟏/𝟑@𝟏/𝟓)] Hence u = 1/2 , v = 1/3 , & w = 1/5 Thus, x = 2, y = 3 & z = 5 Putting u = 𝟏/𝒙 1/2 = 1/𝑥 x = 2 Putting v = 𝟏/𝒚 1/3 = 1/𝑦 y = 3 Putting w = 𝟏/𝒛 1/5 = 1/𝑧 z = 5