Example 7 - Chapter 4 Class 12 Determinants (Important Question)

Transcript

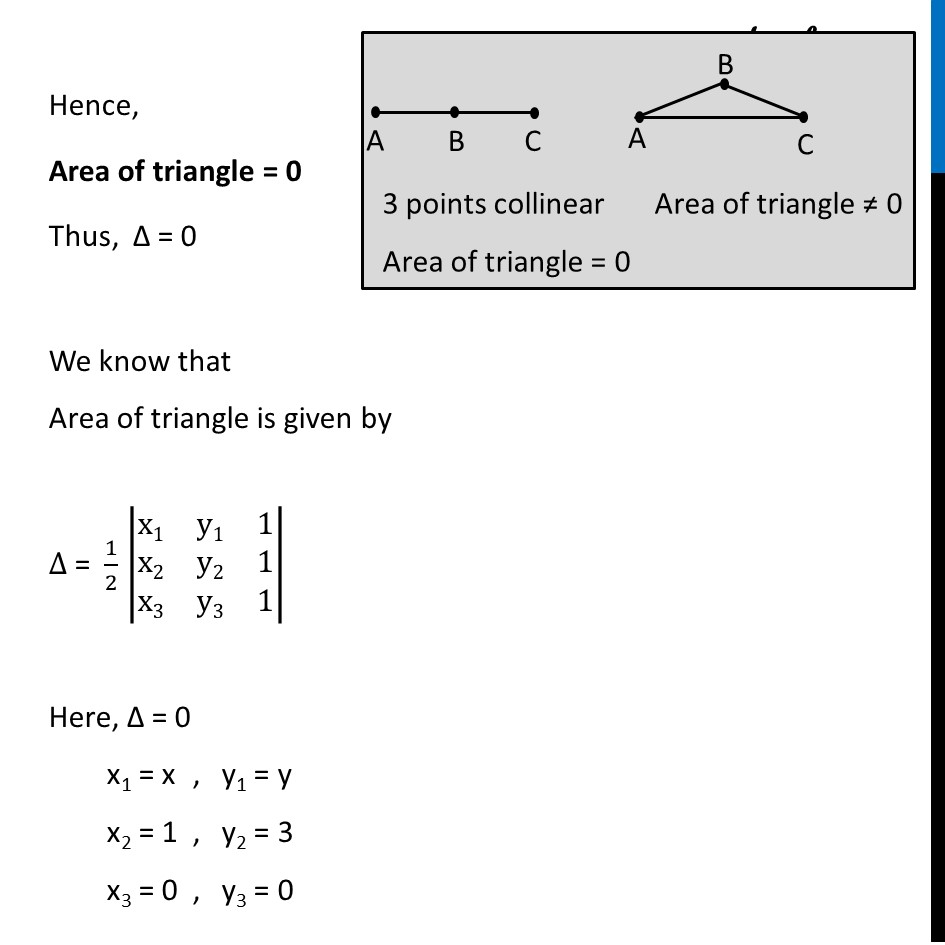
Example 7 Find the equation of the line joining A(1, 3) and B(0, 0) using determinants and find k if D(k, 0) is a point such that area of triangle ABD is 3 sq units. Equation of line Let L be the line joining the A(1, 3) & B(0, 0) Let (x, y) be the third point on line Since all the three points lie on the same line, they do not from a triangle Hence, Area of triangle = 0 Thus, ∆ = 0 We know that Area of triangle is given by ∆ = 1/2 |■8(x1&y1&1@x2&y2&1@x3&y3&1)| Here, ∆ = 0 x1 = x , y1 = y x2 = 1 , y2 = 3 x3 = 0 , y3 = 0 Putting values 0 = 1/2 |■8(𝑥&𝑦&1@1&3&1@0&0&1)| 0 = 1/2 (𝑥|■8(3&1@0&1)|−𝑦|■8(1&1@0&1)|+1|■8(1&3@0&0)|) 0 = 1/2 ( x (3 – 0) – y (1 – 0) +1 (0 – 0)) 0 = 1/2 (x (3) – y (1) + 0) 0 = 1/2 (3x – y) 2 × 0 = 3x – y 0 = 3x – y 3x – y = 0 y = 3x Thus, the equation of line joining A & B is y = 3x Also given a point D (k, 0) & Area of triangle ∆ ABD is 3 square unit Since, Area of triangle is always positive , ∆ can have both positive and negative sings ∴ ∆ = ± 3 We have A (1, 3) : x1 = 1, y1 = 3 B (0, 0) : x2 = 0, y2 = 0 D (k, 0) : x3 = k , y3 = 0 Area of triangle is ∆ = 1/2 |■8(x1&y1&1@x2&y2&1@x3&y3&1)| ± 3 = 1/2 |■8(1&3&1@0&0&1@k&0&1)| ± 3 = 1/2 (1|■8(0&1@0&1)|−3|■8(0&1@k&1)|+1|■8(0&0@k&0)|) ± 3 = 1/2 ( 1 (0 – 0) – 3 (k – 0) +1 (0 – 0)) ±3 = 1/2 (0 – 3 (k) + 0) ±3 = 1/2 ( –3k) ± 6 = –3k So, 6 = –3k or –6 = –3k 6 = –3k 3k = 6 k = 6/(−3) = –2 –6 = – 3k –3k = –6 k = (−6)/(−3) = 2 Hence, the value of k is 2 or –2