Ex 4.3, 2 (i) - Chapter 4 Class 12 Determinants

Transcript

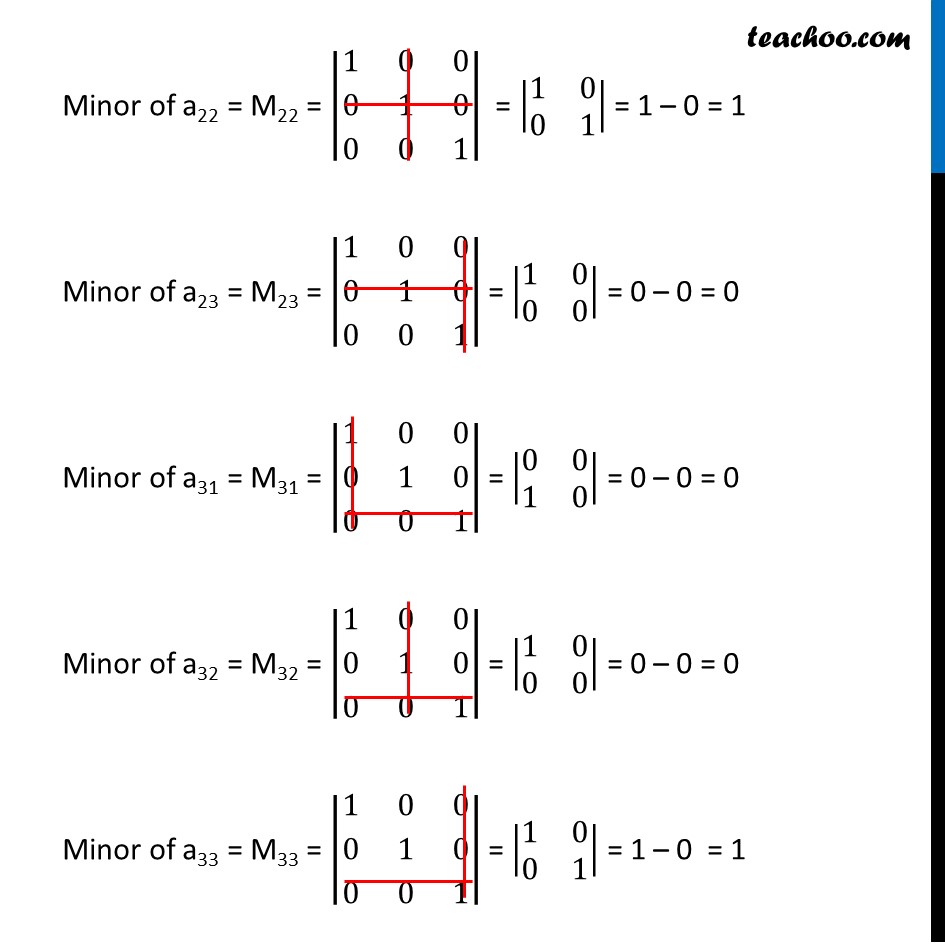
Ex 4.3, 2 Write Minors and Cofactors of the elements of determinants: (i) |■8(1&0&0@0&1&0@0&0&1)| Minor of a11 = M11 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(1&0@0&1)| = 1(1) – 0 = 1 Minor of a12 = M12 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(0&0@0&1)| = 0 – 0 = 0 Minor of a13 = M13 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(0&1@0&0)| = 0 – 0 = 0 Minor of a21 = M21 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(0&0@0&1)| = 0 – 0 = 0 Minor of a22 = M22 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(1&0@0&1)| = 1 – 0 = 1 Minor of a23 = M23 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(1&0@0&0)| = 0 – 0 = 0 Minor of a31 = M31 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(0&0@1&0)| = 0 – 0 = 0 Minor of a32 = M32 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(1&0@0&0)| = 0 – 0 = 0 Minor of a33 = M33 = |■8(1&0&0@0&1&0@0&0&1)| = |■8(1&0@0&1)| = 1 – 0 = 1 Cofactor of a11 = A11 = (–1)1+1 M11= (–1)2 × 1= 1 × 1 = 1 Cofactor of a12 = A12 = (–1)1+2 M12= (–1)3 0 = 0 Cofactor of a13 = A13 = (–1)1+3 M13 = (–1)4 0 = 0 Cofactor of a21 = A21 = (–1)2+1 M21 = (–1)3 0 = 0 Cofactor of a22 = A22 = (–1)2+2 M22 = (–1)4 1 = 1 . 1 = 1 Cofactor of a23 = A23 = (–1)3 + 1 M23 = (–1)4 0 = 0 Cofactor of a31 = A31 = (–1)3 + 1 M31 = (–1)4 0 = 0 Cofactor of a32 = A32 = (–1)3 + 2 M32 = (–1)5 0 = 0 Cofactor of a33 = A33 = (–1)3 + 3 M33 = (–1)6 . 1 = 1 . 1 = 1