Ex 14.2, 18 - Chapter 14 Class 11 Probability

Transcript

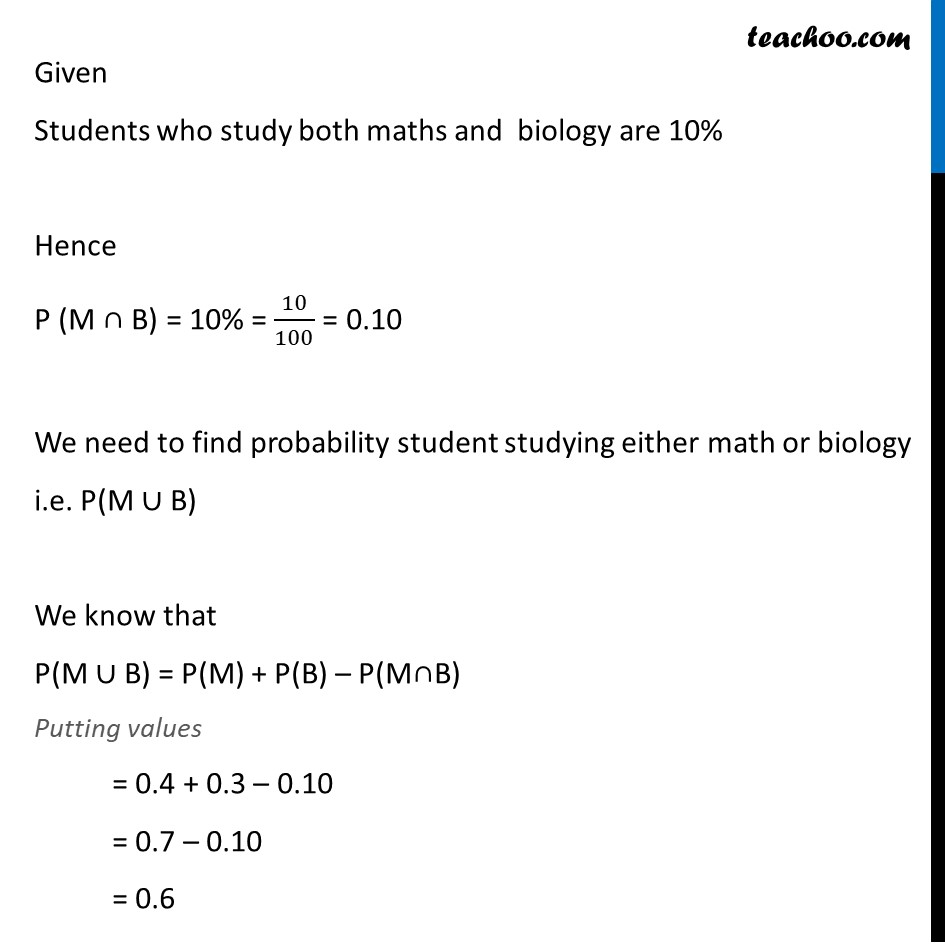
Ex 14.2, 18 In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology. Let B be the event of student studying biology. & M be the event of student studying maths Hence Probability student study maths = 40% P(M) = 40 % = 40﷮100﷯ = 0.4 Probability student study biology = 30% P(B) = 30% = 30﷮100﷯ = 0.3 Given Students who study both maths and biology are 10% Hence P (M ∩ B) = 10% = 10﷮100﷯ = 0.10 We need to find probability student studying either math or biology i.e. P(M ∪ B) We know that P(M ∪ B) = P(M) + P(B) – P(M∩B) Putting values = 0.4 + 0.3 – 0.10 = 0.7 – 0.10 = 0.6 Hence, probability student studying either math or biology = 0.6