Example 13 - Mathematical Reasoning
Last updated at Dec. 16, 2024 by Teachoo
Examples
Example 1 (i)
You are here
You are here
Transcript
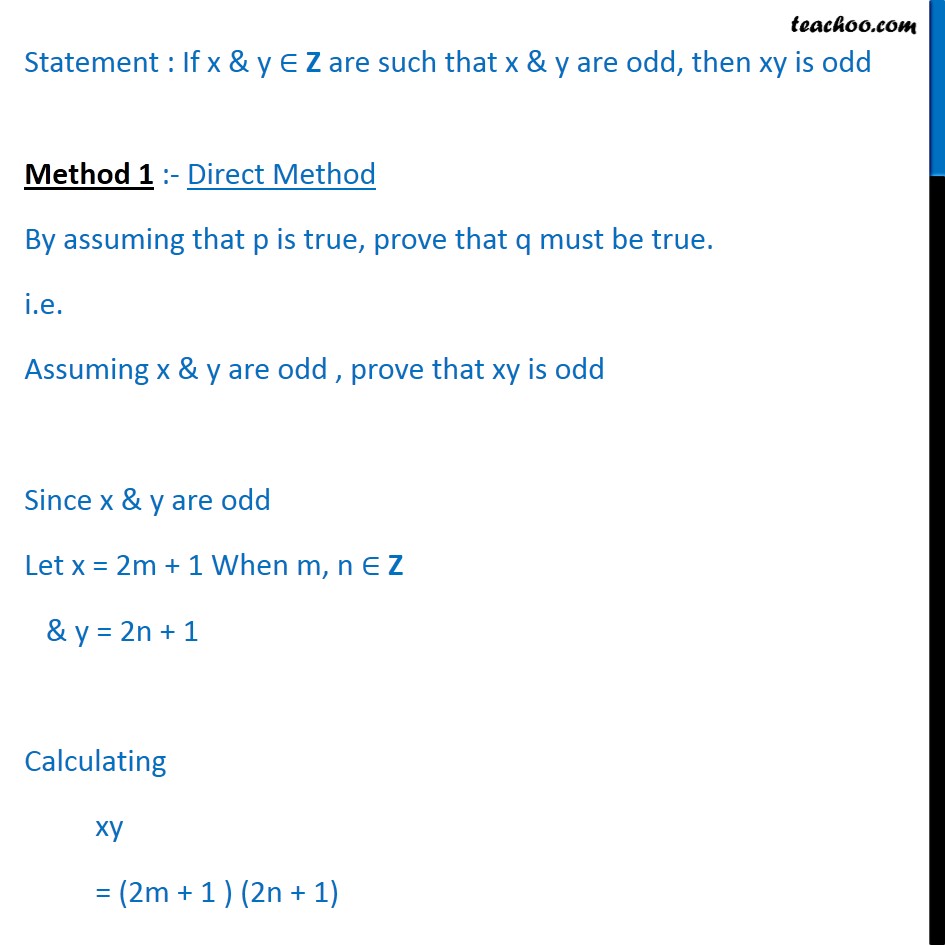
Example 13 Check whether the following statement is true or not. If x, y ∈ Z are such that x and y are odd, then xy is odd. Statement : If x & y ∈ Z are such that x & y are odd, then xy is odd Let p : x , y ∈ Z such . that x and y are odd q : xy is odd That given statement is of the form if p ⇒ q We check the validity of the given statement Statement : If x & y ∈ Z are such that x & y are odd, then xy is odd Method 1 :- Direct Method By assuming that p is true, prove that q must be true. i.e. Assuming x & y are odd , prove that xy is odd Since x & y are odd Let x = 2m + 1 When m, n ∈ Z & y = 2n + 1 Calculating xy = (2m + 1 ) (2n + 1) = 2m (2n + 1 ) + 1 (2n + 1 ) = (2m) (2n) + 2m + 2n + 1 = 4mn + 2m + 2n + 1 = 2 (mn + m + n) + 1 This shows xy is odd Hence q is true. Therefore the given statement is true Method 2 :- Contrapositive Method Statement : If x & y ∈ Z are such that x & y are odd, then xy is odd By assuming that q is false, prove that p must be false. Let xy be not odd , prove that x and y are not odd Since xy is not odd ⇒ xy is even. ⇒ This is possible only if either x or y is even Let us take an example
