Ex 12.1, 22 - Chapter 13 Class 11 Limits and Derivatives (Important Question)

Transcript

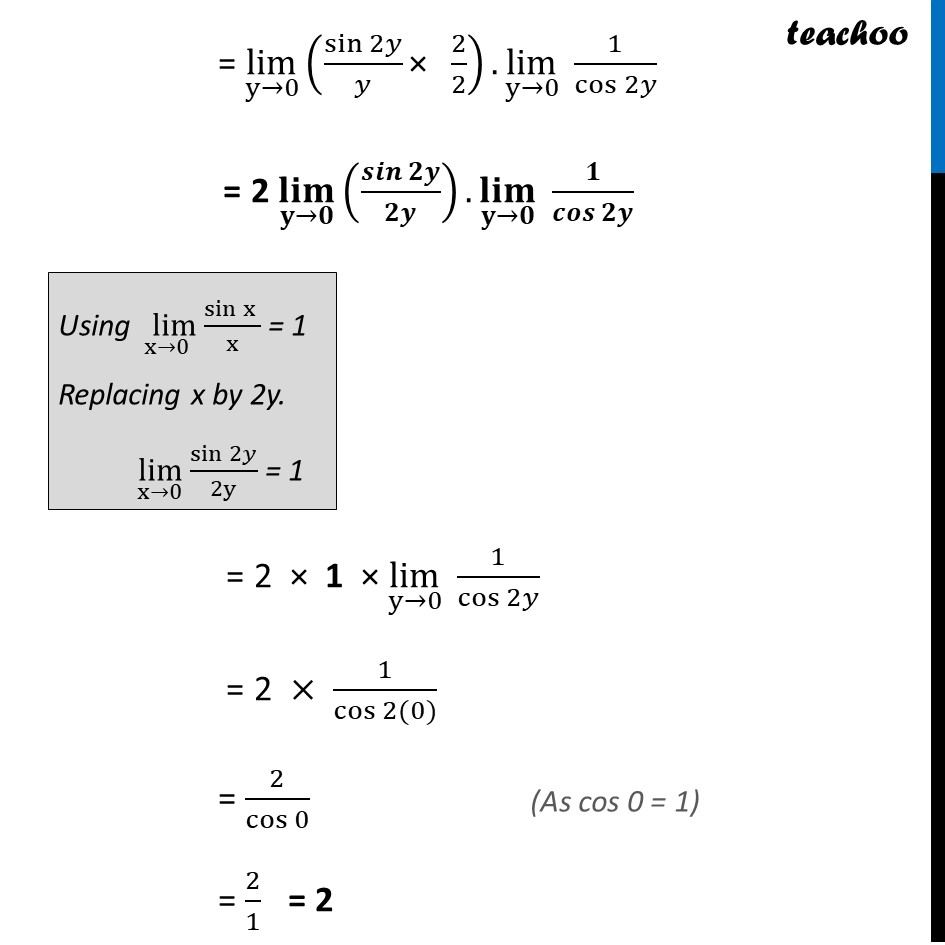
Ex 12.1, 22 lim┬(x → π/2) tan⁡2x/(x − π/2) lim┬(x → π/2) tan⁡2x/(x − π/2) Putting y = x – π/2 When x → 𝜋/2 y → 𝜋/2 – 𝜋/2 y → 0 So, our equation becomes lim┬(x→π/2) tan⁡2x/(x − π/2) = lim┬(y→0) (tan⁡2(𝜋/2 + 𝑦)/𝑦) = lim┬(y→0) ((〖tan 〗⁡〖(𝜋 + 2𝑦〗))/𝑦) = lim┬(y→0) (tan⁡2𝑦/𝑦) = lim┬(y→0) (1/𝑦 . sin⁡2𝑦/cos⁡2𝑦 ) = lim┬(y→0) (sin⁡2𝑦/𝑦 . 1/cos⁡2𝑦 ) = lim┬(y→0) sin⁡2𝑦/𝑦 ×lim┬(y→0) 1/cos⁡2𝑦 Multiply & Divide by 2 (As tan⁡〖(𝜋+𝑥〗)=tan x) = lim┬(y→0) (sin⁡2𝑦/𝑦 "× " 2/2).lim┬(y→0) 1/cos⁡2𝑦 = 2 lim┬(y→0) (𝒔𝒊𝒏⁡𝟐𝒚/𝟐𝒚).lim┬(y→0) 1/cos⁡2𝑦 Using ( lim)┬(x→0) (sin⁡x )/x = 1 Replacing x by 2y. lim┬(x→0) sin⁡2𝑦/2y = 1 = 2 × 1 × lim┬(y→0) 1/cos⁡2𝑦 = 2 × 1/cos⁡〖2(0)〗 = 2/cos⁡0 = 2/1 = 2 (As cos 0 = 1)