Ex 12.1, 14 - Chapter 12 Class 11 Limits and Derivatives

Transcript

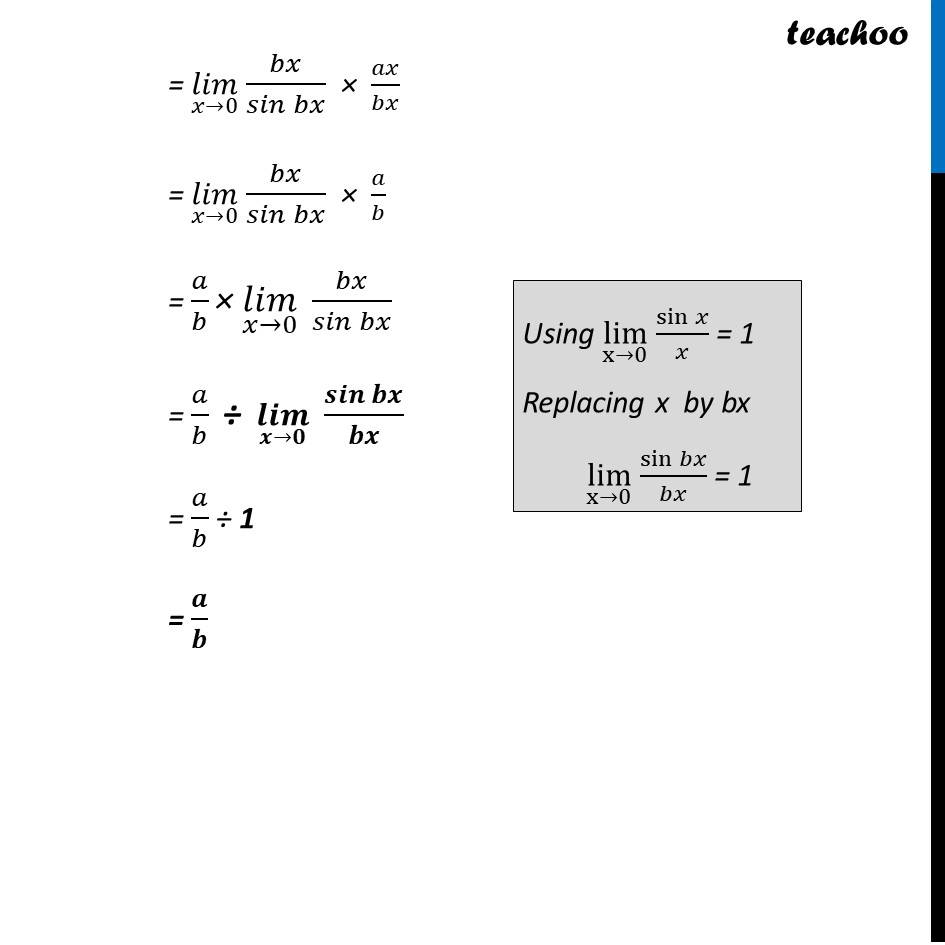
Ex 12.1, 14 Evaluate the Given limit: lim┬(x→0) sin⁡〖ax 〗/(sin bx), a, b ≠ 0 (𝑙𝑖𝑚)┬(𝑥→0) 𝑠𝑖𝑛⁡〖𝑎𝑥 〗/(𝑠𝑖𝑛 𝑏𝑥) = (𝑙𝑖𝑚)┬(𝑥→0) sin ax × (𝑙𝑖𝑚)┬(𝑥→0) 1/𝑠𝑖𝑛⁡𝑏𝑥 Multiplying & dividing by ax = (𝒍𝒊𝒎)┬(𝒙→𝟎) 𝒔𝒊𝒏⁡𝒂𝒙/𝒂𝒙 × (𝑙𝑖𝑚)┬(𝑥→0) 𝑎𝑥/𝑠𝑖𝑛⁡𝑏𝑥 = 1 × (𝑙𝑖𝑚)┬(𝑥→0) 𝑎𝑥/𝑠𝑖𝑛⁡𝑏𝑥 = (𝑙𝑖𝑚)┬(𝑥→0) 𝑎𝑥/𝑠𝑖𝑛⁡𝑏𝑥 Multiplying & dividing by bx = (𝑙𝑖𝑚)┬(𝑥→0) 𝑎𝑥/𝑠𝑖𝑛⁡𝑏𝑥 × 𝑏𝑥/𝑏𝑥 Using lim┬(x→0) sin⁡𝑥/𝑥 = 1 Replacing x by ax lim┬(x→0) sin⁡𝑎𝑥/𝑎𝑥 = 1 = (𝑙𝑖𝑚)┬(𝑥→0) 𝑏𝑥/𝑠𝑖𝑛⁡𝑏𝑥 × 𝑎𝑥/𝑏𝑥 = (𝑙𝑖𝑚)┬(𝑥→0) 𝑏𝑥/𝑠𝑖𝑛⁡𝑏𝑥 × 𝑎/𝑏 = 𝑎/𝑏 "×" (𝑙𝑖𝑚)┬(𝑥→0) 𝑏𝑥/𝑠𝑖𝑛⁡𝑏𝑥 = 𝑎/𝑏 ÷ (𝒍𝒊𝒎)┬(𝒙→𝟎) 𝒔𝒊𝒏⁡𝒃𝒙/𝒃𝒙 = 𝑎/𝑏 ÷ 1 = 𝒂/𝒃 Using lim┬(x→0) sin⁡𝑥/𝑥 = 1 Replacing x by bx lim┬(x→0) sin⁡𝑏𝑥/𝑏𝑥 = 1