Ex 12.1,10 - Chapter 13 Class 11 Limits and Derivatives (Important Question)

Transcript

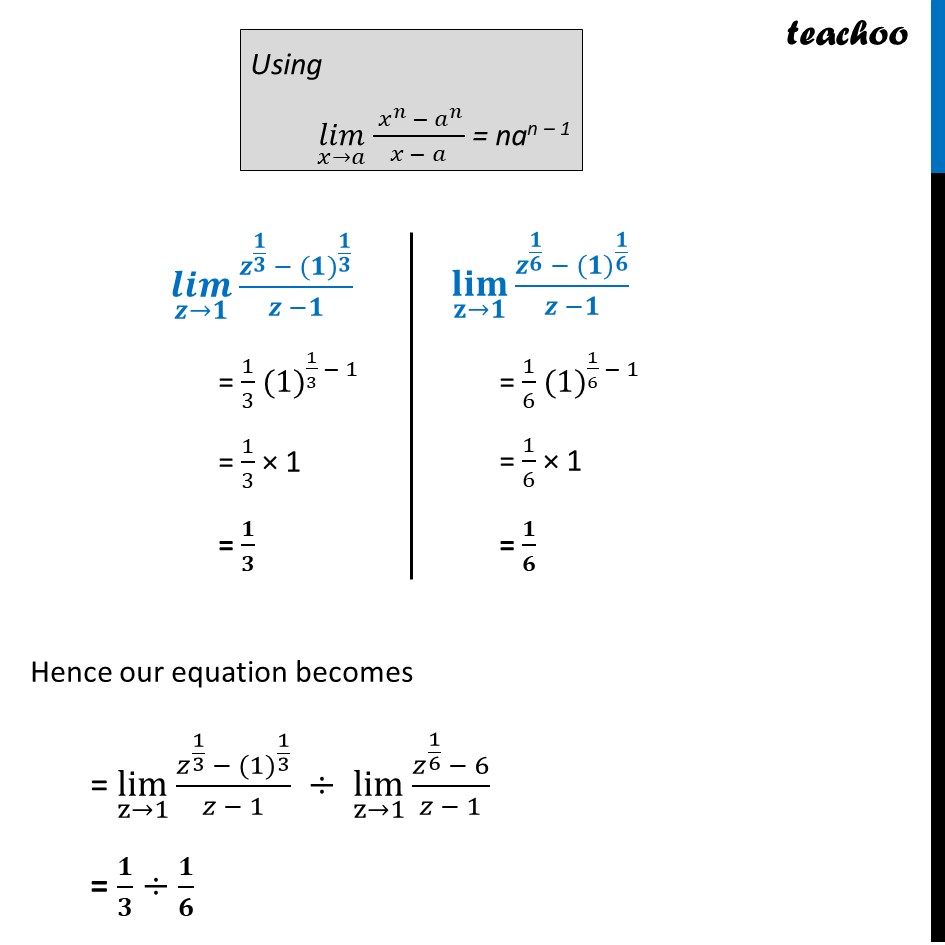
Ex 12.1, 10 Evaluate the Given limit: lim┬(z→1) (𝑧^(1/3) − 1)/(𝑧^(1/6) − 1) lim┬(z→1) (𝑧^(1/3) − 1)/(𝑧^(1/6) − 1) = (〖(1)〗^(1/3) − 1)/(〖(1)〗^(1/6) − 1) = (1 − 1)/(1 − 1) = 0/0 Since it is form 0/0, We can solve it by using (𝑙𝑖𝑚)┬(𝑥→𝑎) (𝑥^𝑛 − 𝑎^𝑛)/(𝑥 − 𝑎) = nan – 1 Hence, lim┬(z→1) (𝑧^(1/3) − 1)/(𝑧^(1/6) − 1) = lim┬(z→1) 𝑧^(1/3) – 1 ÷ lim┬(z→1) 𝑧^(1/6) − 1 = lim┬(z→1) 𝑧^(1/3) – 〖(1)〗^(1/3) ÷ lim┬(z→1) 𝑧^(1/6) – 〖(1)〗^(1/6) Multiplying and dividing by z – 1 = lim┬(z→1) (𝑧^(1/3) − 〖(1)〗^(1/3))/(𝑧 − 1) ÷ lim┬(z→1) (𝑧^(1/6) −〖 (1)〗^(1/6))/(𝑧 − 1) Using (𝑙𝑖𝑚)┬(𝑥→𝑎) ( 𝑥^𝑛 − 𝑎^𝑛)/(𝑥 − 𝑎) = nan – 1 lim┬(z→1) (𝑧^(1/3) − 〖(1)〗^(1/3))/(𝑧 −1) = 1/3 〖(1)〗^(1/3 − 1) = 1/3 × 1 = 1/3 lim┬(z→1) (𝑧^(1/6) − 〖(1)〗^(1/6))/(𝑧 −1) = 1/6 〖(1)〗^(1/6 − 1) = 1/6 × 1 = 1/6 Hence our equation becomes = lim┬(z→1) (𝑧^(1/3) − 〖(1)〗^(1/3))/(𝑧 − 1) ÷ lim┬(z→1) (𝑧^(1/6) − 6)/(𝑧 − 1) = 1/3 ÷1/6 = 1/3 × 6/1 = 2