
Last updated at December 16, 2024 by Teachoo




Transcript
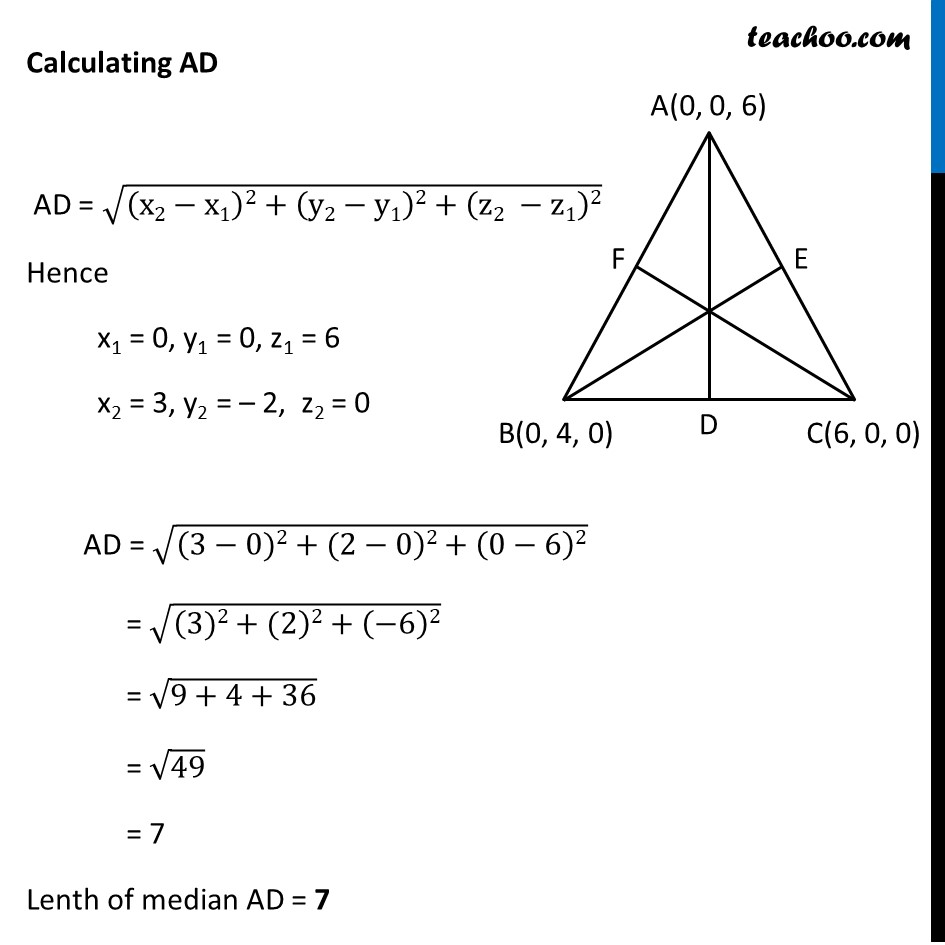
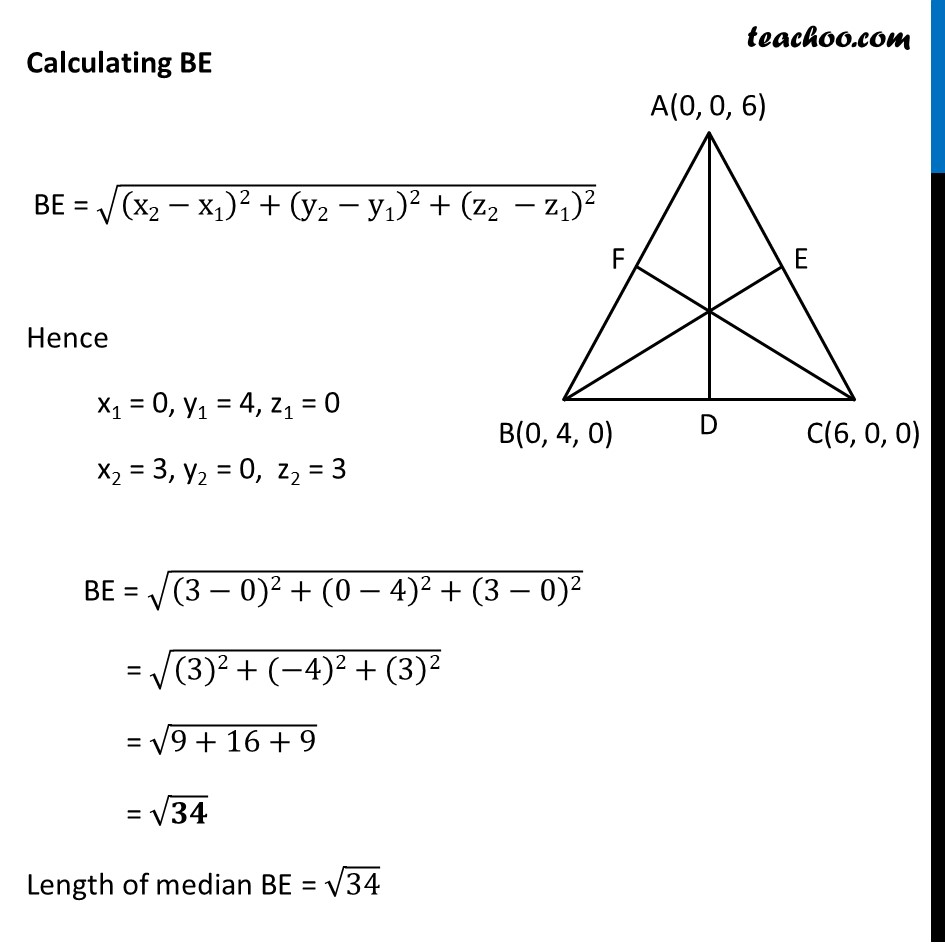
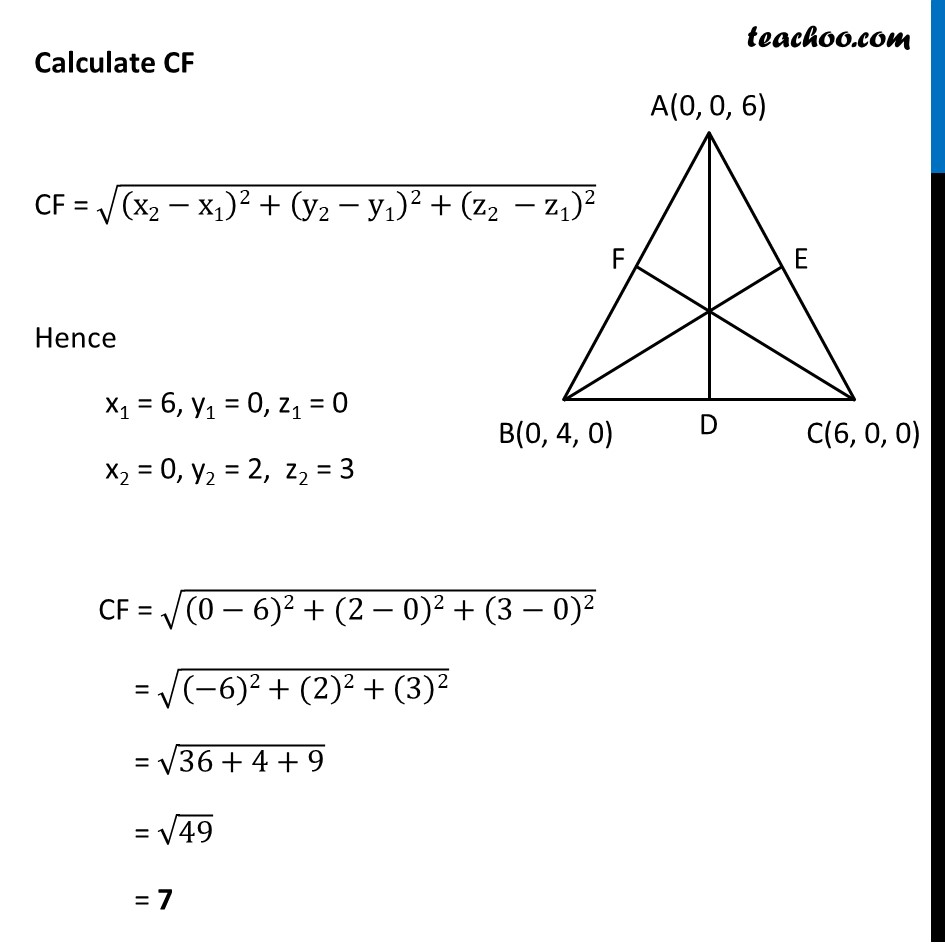
Misc 2 Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0). Let Δ ABC where AD, BE, CF are medians Since median bisects the opposite side D is Midpoint of BC E is Midpoint of AC F Midpoint of AB Misc 2 Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0). Let Δ ABC where AD, BE, CF are medians Since median bisects the opposite side D is Midpoint of BC E is Midpoint of AC F Midpoint of AB E is midpoint of AC D = ((0 + 6)/2, (0 + 0)/2, (6 + 0)/2) D = (3, 0, 3) F is midpoint of AB D = ((0 + 0)/2, (0 + 4)/2, (6 + 0)/2) D = (0, 2, 3) Calculating AD AD = √((x2−x1)2+(y2−y1)2+(z2 −z1)2) Hence x1 = 0, y1 = 0, z1 = 6 x2 = 3, y2 = – 2, z2 = 0 AD = √((3−0)2+(2−0)2+(0−6)2) = √((3)2+(2)2+(−6)2) = √(9+4+36) = √49 = 7 Lenth of median AD = 7 Calculating BE BE = √((x2−x1)2+(y2−y1)2+(z2 −z1)2) Hence x1 = 0, y1 = 4, z1 = 0 x2 = 3, y2 = 0, z2 = 3 BE = √((3−0)2+(0−4)2+(3−0)2) = √((3)2+(−4)2+(3)2) = √(9+16+9) = √𝟑𝟒 Length of median BE = √34 Calculate CF CF = √((x2−x1)2+(y2−y1)2+(z2 −z1)2) Hence x1 = 6, y1 = 0, z1 = 0 x2 = 0, y2 = 2, z2 = 3 CF = √((0−6)2+(2−0)2+(3−0)2) = √((−6)2+(2)2+(3)2) = √(36+4+9) = √49 = 7