Misc 7 - Chapter 10 Class 11 Conic Sections

Transcript

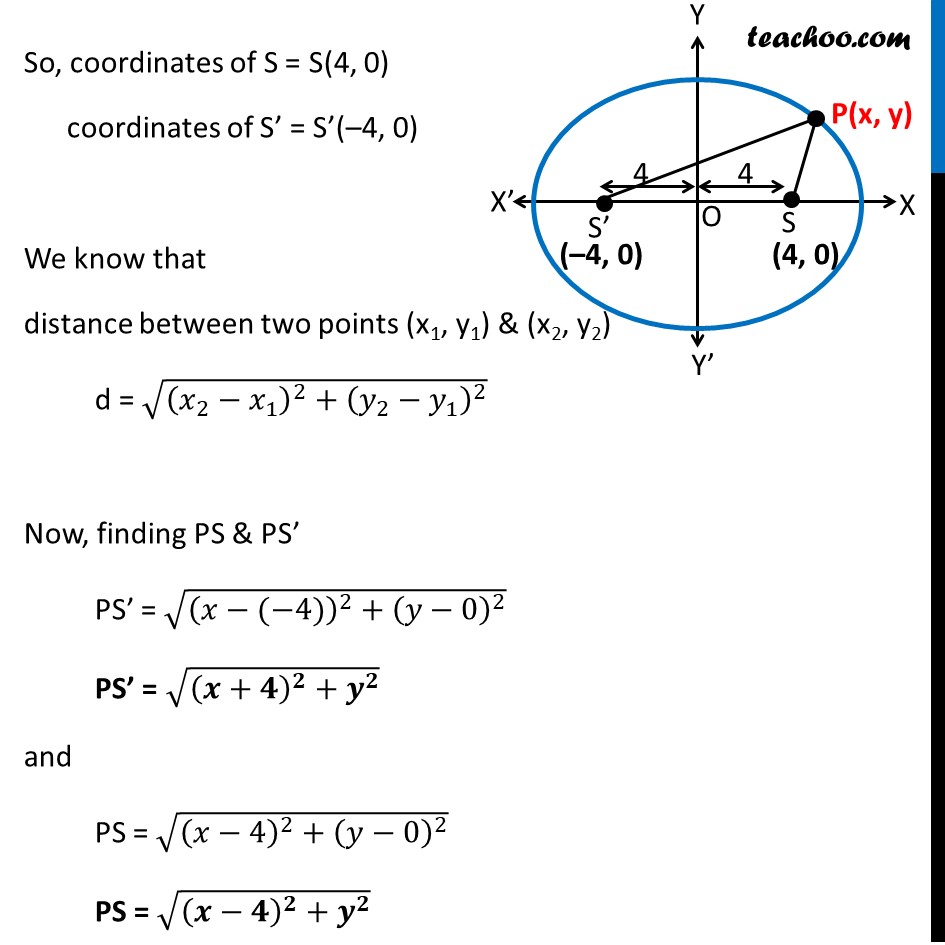
Misc 7(Method 1) A man running a racecourse notes that the sum of the distances from the two flag posts from him is always 10 m and the distance between the flag posts is 8 m. find the equation of the posts traced by the man. Let man be standing on point P(x, y) There are two flag posts S & S Given PS + PS = 10 & SS = 8 m Let S & S be on x-axis such that Origin (O) be the mid-point of S S So, OS = OS = 4 m So, coordinates of S = S(4, 0) coordinates of S = S ( 4, 0) We know that distance between two points (x1, y1) & (x2, y2) d = 2 1 2 + 2 1 2 Now, finding PS & PS PS = ( 4) 2 + 0 2 PS = +4 2 + 2 and PS = 4 2 + 0 2 PS = 4 2 + 2 Now, PS + PS = 10 Putting values 4 2 + 2 + +4 2 + 2 = 10 4 2 + 2 = 10 +4 2 + 2 Squaring both sides 4 2 + 2 2 = 10 +4 2 + 2 2 4 2 + 2 = 102 + +4 2 + 2 2 20 +4 2 + 2 4 2 + 2 = 100 + +4 2 + 2 20 +4 2 + 2 x2 + 42 8x + 2 = 100 + x2 + 42 + 8x + 2 20 +4 2 + 2 x2 + 42 8x + 2 100 x2 42 8x 2 = 20 +4 2 + 2 16x 100 = 20 +4 2 + 2 20 +4 2 + 2 = 16x + 100 20 +4 2 + 2 = 4(4x + 25) 5 +4 2 + 2 = (4x + 25) Squaring both sides 5 +4 2 + 2 2 = (4x + 25)2 25 +4 2 + 2 = (4x + 25)2 25(x2 + 42 + 8x + y2) = (4x)2 + (25)2 + 2(4x)(25) 25x2 + 400 + 200x + 25y2 = 16x2 + 625 + 200x 9x2 + 25y2 = 225 9 2 225 + 25 2 225 = 1 + = 1 Misc 7(Method 2) A man running a racecourse notes that the sum of the distances from the two flag posts form him is always 10 m and the distance between the flag posts is 8 m. find the equation of the posts traced by the man. Let S & S be two flag past The sum of distance of man P from S & S is equal to 10 Since the sum of distance of a point from any two fixed points S & S in the plane is constant, it forms on ellipse. So, S & S are the foci of the ellipse x-axis is the major axis, y-axis is the minor axis Let equation of ellipse be 2 2 + 2 2 = 1 Now, given that The sum of distance of man P from S & S = 10 i.e. Sum of distance of a point from foci is = 10 2a = 10 m a = 10 2 = 5m Also it is given that Distance between flag posts SS = 8m Distance between two foci = 8 m 2c = 8 c = 8 2 = 4 Now we need to find b We know that c2 = a2 b2 42 = 52 b2 16 = 25 b2 b2 = 25 16 b2 = 9 b = 3 Now equation of ellipse is 2 2 + 2 2 = 1 2 5 2 + 2 3 2 = 1 + = 1 Thus, the required equation is 2 25 + 2 9 = 1