

Last updated at December 16, 2024 by Teachoo



Transcript
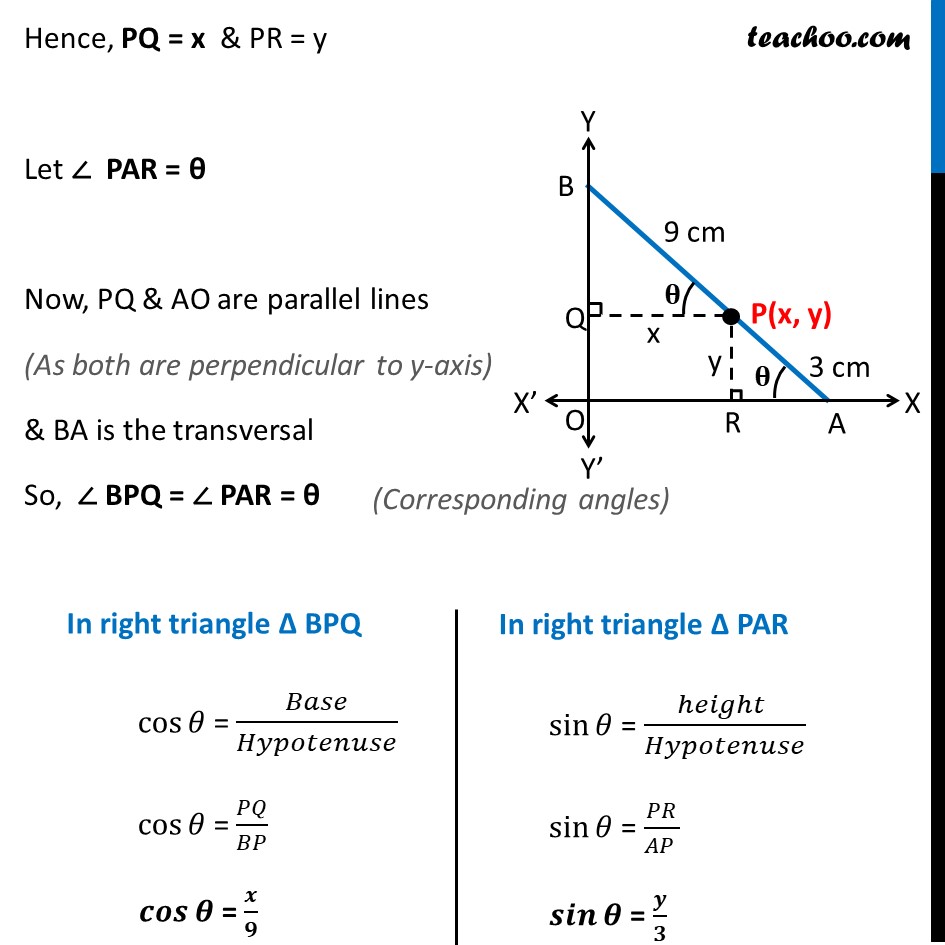
Misc, 5 A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis. Let AB be the rod where A touches the x-axis & B touches the y-axis Let point P(x, y) Given AB = Length of rod = 12 cm & AP = 3 cm PB = AB – AP PB = 12 – 3 = 9cm Drawing PQ ⊥ BO and PR ⊥ OA Hence, PQ = x & PR = y Let ∠ PAR = θ Now, PQ & AO are parallel lines (As both are perpendicular to y-axis) & BA is the transversal So ∠ BPQ = ∠ PAR = θ Now we know that, sin2𝜃 + cos2𝜃 = 1 Putting 𝑠𝑖𝑛𝜃 = 𝑦6 and 𝑐𝑜𝑠𝜃 = 𝑥9 𝑦32 + 𝑥92 = 1 𝑦29 + 𝑥281 = 1 𝒙𝟐𝟖𝟏 + 𝒚𝟐𝟗 = 1 Hence it satisfies the equation of ellipse 𝑥2𝑎2 + 𝑦2𝑏2 = 1 Thus locus of P is ellipse