Misc 3 - Chapter 10 Class 11 Conic Sections

Transcript

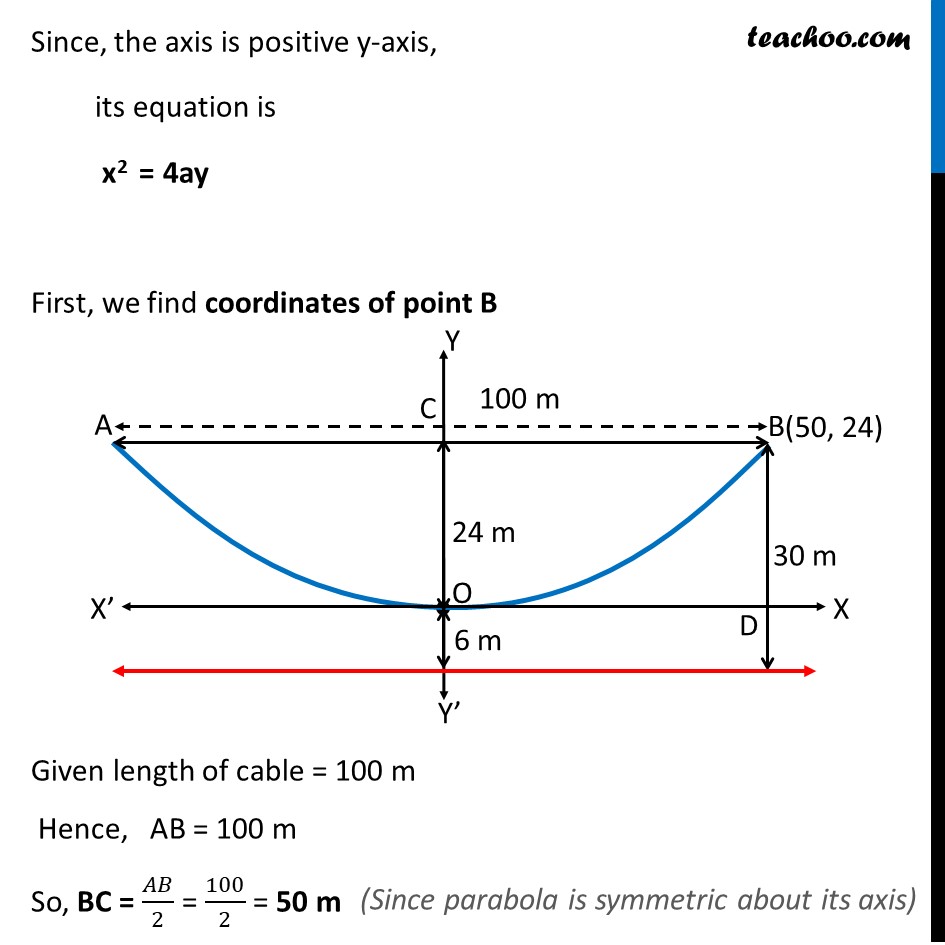
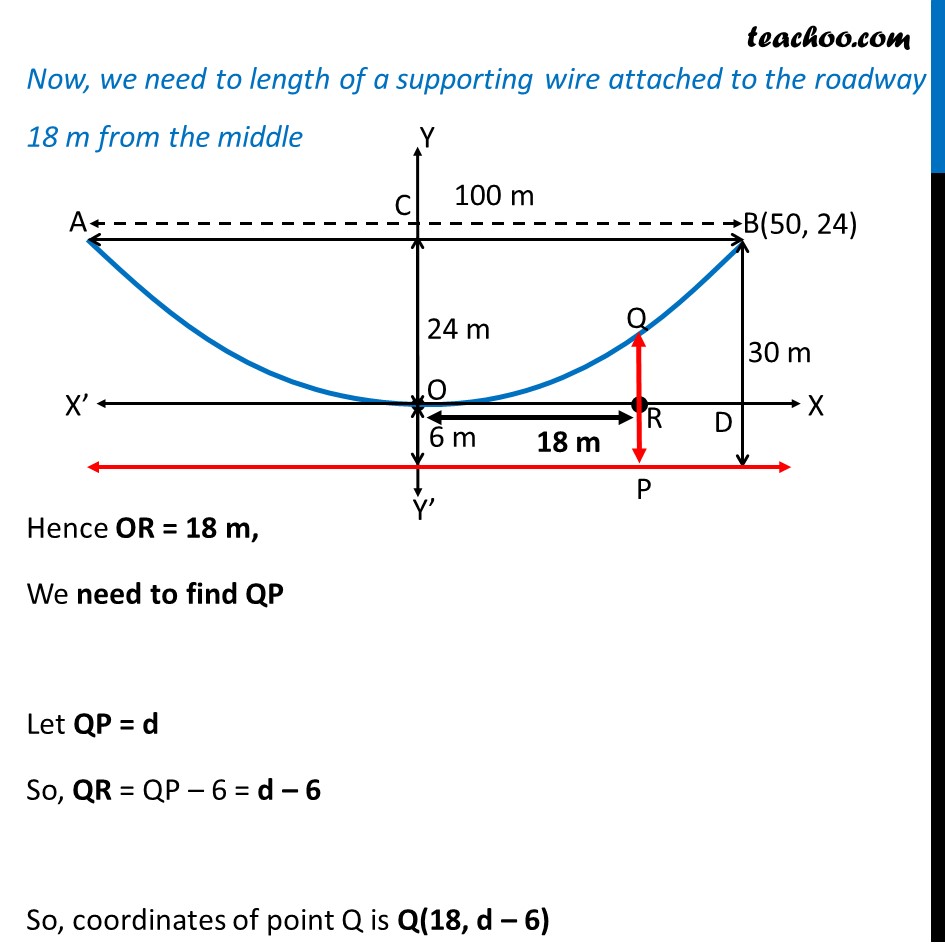
Misc 3 The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle. Cable is always facing upwards with the axis vertical Since, the axis is positive y-axis, its equation is x2 = 4ay First, we find coordinates of point B Given length of cable = 100 m Hence, AB = 100 m So, BC = 2 = 100 2 = 50 m Also, DB = 30 6 = 24 m Hence point B is B (50, 24) Now, Since point B(50, 24) lies on the parabola Putting x = 50, y = 24 in equation of parabola x2 = 4ay (50)2 = 4a (24) 2500 = 4a 24 4a 24 = 2500 4a = 2500 24 4a = 625 6 a = Now, we need to length of a supporting wire attached to the roadway 18 m from the middle Hence OR = 18 m, We need to find QP Let QP = d So, QR = QP 6 = d 6 So, coordinates of point Q is Q(18, d 6) So, coordinates of point Q is Q(18, d 6) Since point Q lies on parabola it will satisfy the equation of parabola Equation of parabola is x2 = 4ay Putting x = 18 & y = d 6 & a = 625 24 182 = 4 625 24 (d 6) 18 18 = 4 625 24 (d 6) 18 18 24 4 625 = (d 6) (d 6) = 18 18 24 4 625 (d 6) = 3.11 d = 6 + 3.11 d = 9.11 So, QP = 9.11 m Length of support is 9.11 m.