Misc 2 - Chapter 10 Class 11 Conic Sections

Transcript

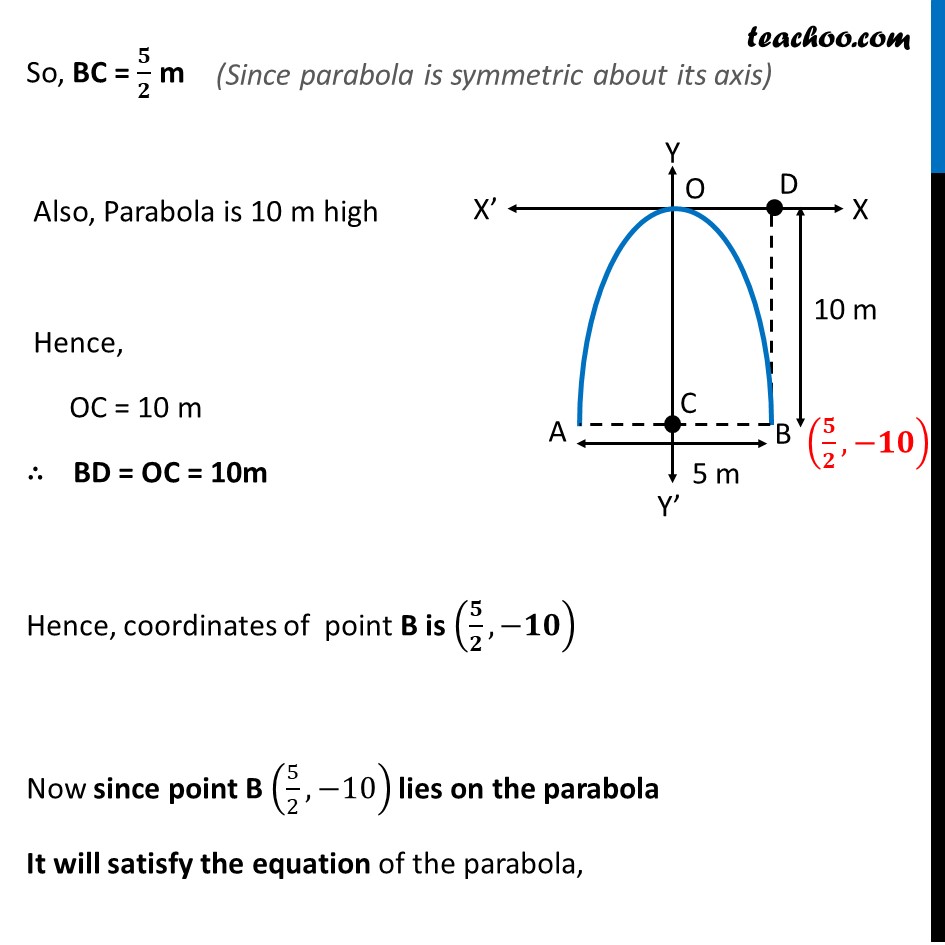
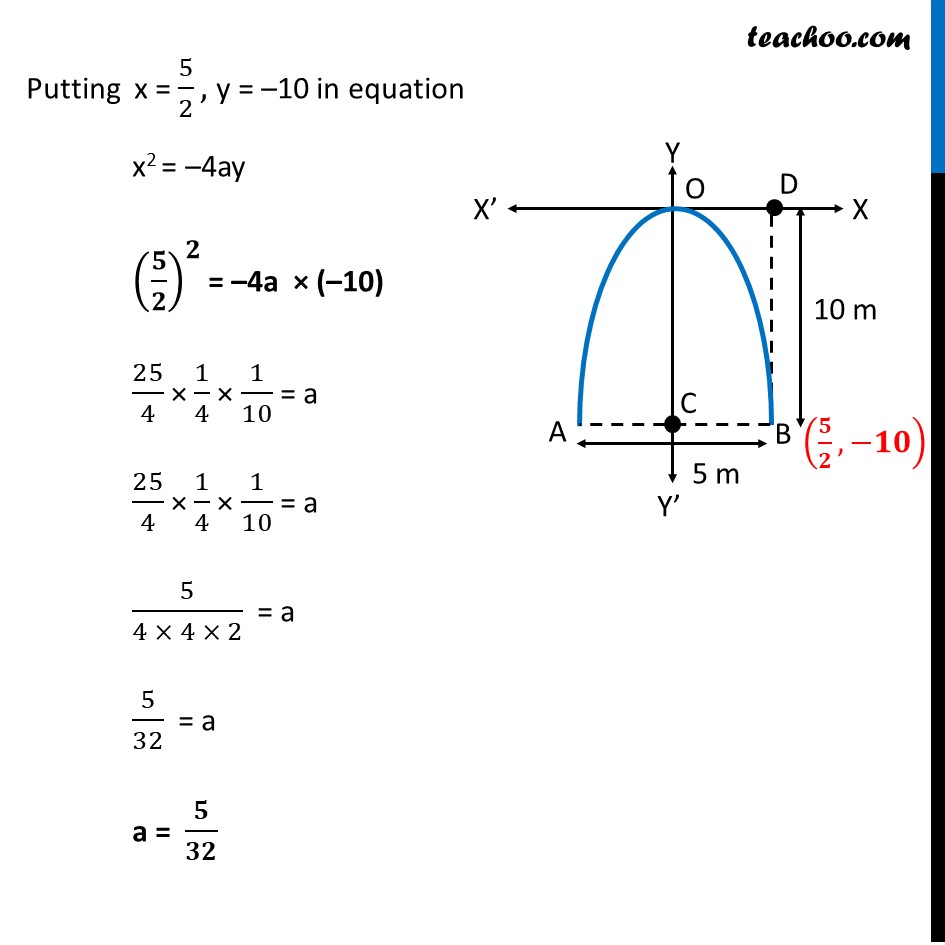
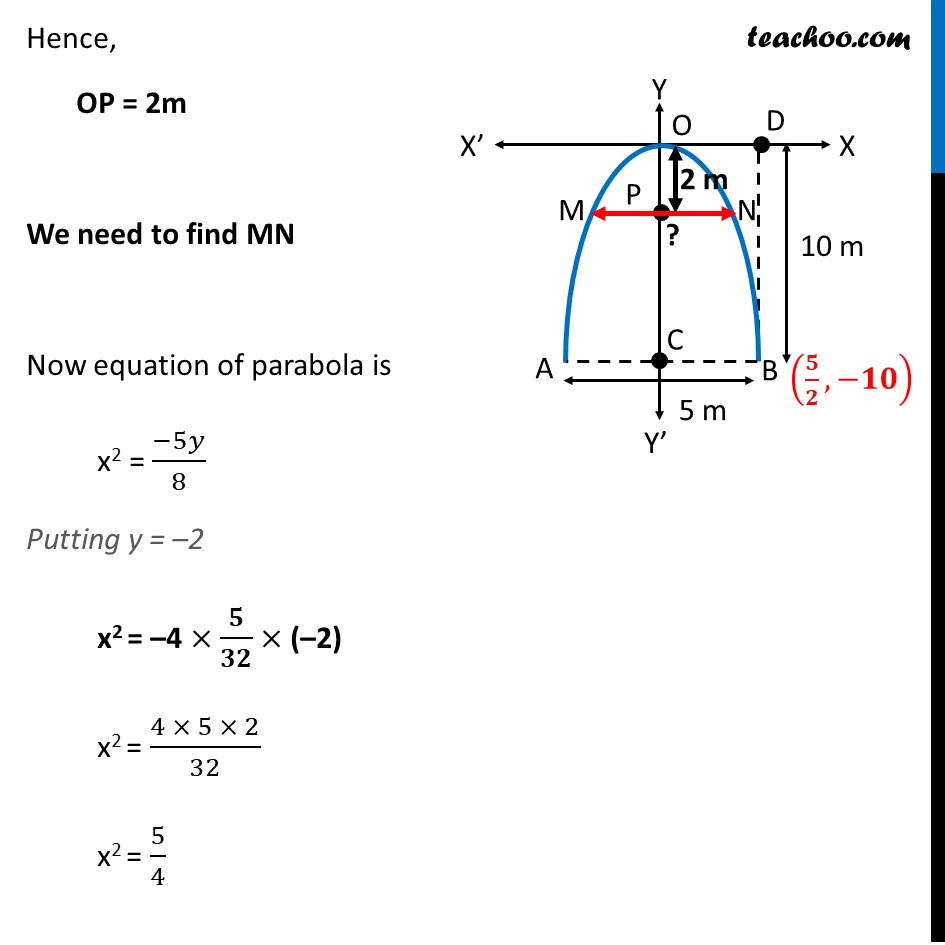
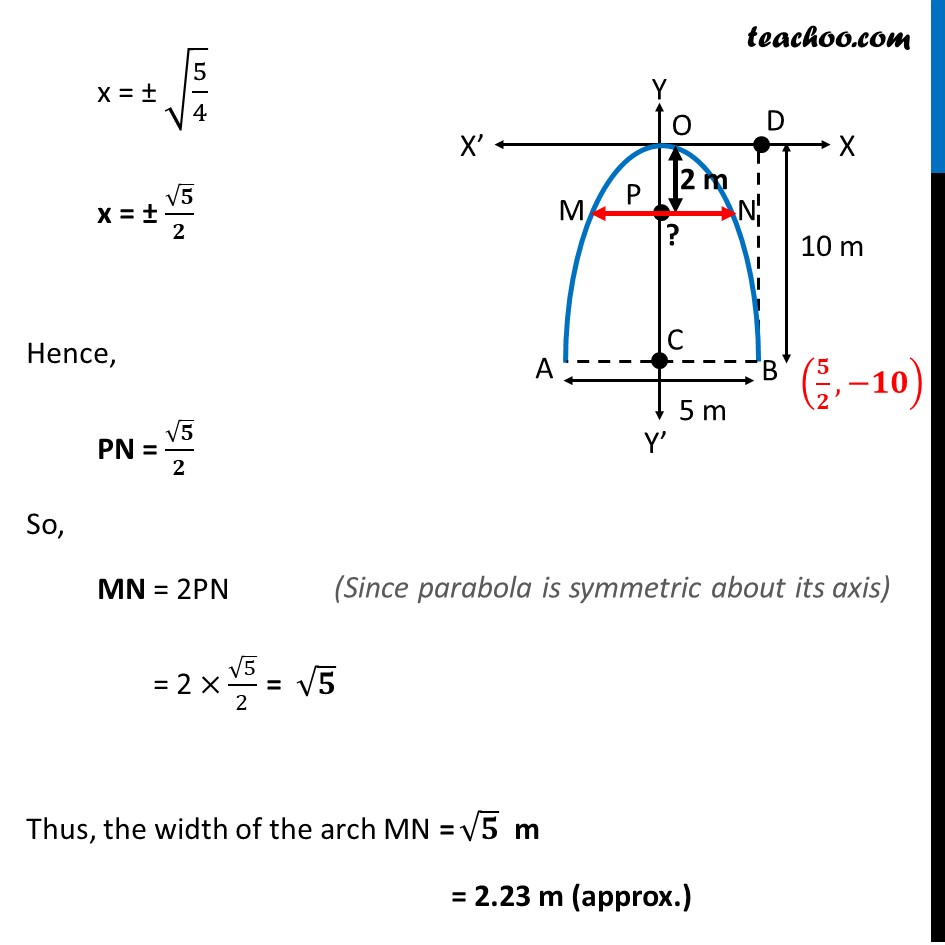
Misc 2 An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola? Arch is downwards, Since, the axis of parabola is negative y-axis, its equation is x2 = 4ay First, we find coordinates of point B Given, Width of Parabola = AB = 5m So, BC = 5 2 m Also, Parabola is 10 m high Hence, OC = 10 m BD = OC = 10m Hence, coordinates of point B is , Now since point B 5 2 , 10 lies on the parabola It will satisfy the equation of the parabola, Putting x = 5 2 , y = 10 in equation x2 = 4ay 5 2 2 = 4a ( 10) 25 4 1 4 1 10 = a 25 4 1 4 1 10 = a 5 4 4 2 = a 5 32 = a a = Hence, the equation of parabola is x2 = 4ay Putting a = 5 32 x2 = 4 5 32 y x2 = We need to find how wide the arch is it 2 m from the vertex of the parabola Let point P be point 2 m from vertex of parabola Hence, OP = 2m We need to find MN Now equation of parabola is x2 = 5 8 Putting y = 2 x2 = 4 5 32 ( 2) x2 = 4 5 2 32 x2 = 5 4 x = 5 4 x = Hence, PN = 5 2 So, MN = 2PN = 2 5 2 = 5 Thus, the width of the arch MN = m = 2.23 m (approx.)